|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
A quadratic recurrence is a Recurrence Relation on a Sequence of numbers ![]() expressing
expressing ![]() as a
second degree polynomial in
as a
second degree polynomial in ![]() with
with ![]() . For example,
. For example,
| (1) |
| (2) |
| (3) |
| (4) |
![\begin{displaymath}
c=\mathop{\rm exp}\nolimits \left[{\,\sum_{j=0}^\infty 2^{-j-1}\ln(1+{y_j}^{-2})}\right]=1.502836801\ldots
\end{displaymath}](q_454.gif) |
(5) |
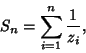 |
(6) |
| (7) |
| (8) |
![\begin{displaymath}
d={\textstyle{1\over 2}}\sqrt{6}\,\mathop{\rm exp}\nolimits ...
...infty 2^{-j-1}\ln[1+(2z_j-1)^{-2}]}\right\}=1.2640847353\ldots
\end{displaymath}](q_461.gif) |
(9) |
| (10) |
See also Mandelbrot Set, Recurrence Relation
References
Aho, A. V. and Sloane, N. J. A. ``Some Doubly Exponential Sequences.'' Fib. Quart. 11, 429-437, 1973.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/quad/quad.html
|
|
|
© 1996-9 Eric W. Weisstein