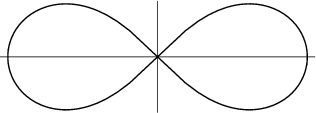
A polar curve also called Lemniscate of Bernoulli which is the Locus of points the product of whose distances
from two points (called the Foci) is a constant. Letting the Foci be located at 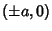 , the Cartesian equation is
, the Cartesian equation is
![\begin{displaymath}[(x-a)^2+y^2][(x+a)^2+y^2]=a^4,
\end{displaymath}](l1_1484.gif) |
(1) |
which can be rewritten
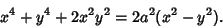 |
(2) |
Letting
 , the Polar Coordinates are given by
, the Polar Coordinates are given by
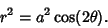 |
(3) |
An alternate form is
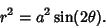 |
(4) |
The parametric equations for the lemniscate are
The bipolar equation of the lemniscate is
 |
(7) |
and in Pedal Coordinates with the Pedal Point at the center, the equation is
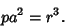 |
(8) |
The two-center Bipolar Coordinates equation with origin at a Focus is
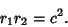 |
(9) |
Jakob Bernoulli  published an article in Acta Eruditorum in 1694 in which he called
this curve the lemniscus (``a pendant ribbon''). Jakob Bernoulli was not aware that the curve he was describing was a
special case of Cassini Ovals which had been described by Cassini
published an article in Acta Eruditorum in 1694 in which he called
this curve the lemniscus (``a pendant ribbon''). Jakob Bernoulli was not aware that the curve he was describing was a
special case of Cassini Ovals which had been described by Cassini  in 1680. The general properties of
the lemniscate were discovered by G. Fagnano in 1750 (MacTutor Archive). Gauss's
in 1680. The general properties of
the lemniscate were discovered by G. Fagnano in 1750 (MacTutor Archive). Gauss's  and
Euler's
and
Euler's  investigations of the Arc Length of the curve led to later work on Elliptic
Functions.
investigations of the Arc Length of the curve led to later work on Elliptic
Functions.
The Curvature of the lemniscate is
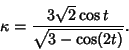 |
(10) |
The Arc Length is more problematic. Using the polar form,
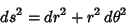 |
(11) |
so
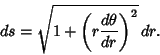 |
(12) |
But we have
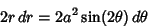 |
(13) |
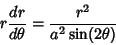 |
(14) |
![\begin{displaymath}
\left({r {d\theta\over dr}}\right)^2 = {r^4\over a^4\sin^2(2...
...ta)} = {r^4\over a^4[1-\cos^2(2\theta)]} = {r^4\over a^4-r^4},
\end{displaymath}](l1_1499.gif) |
(15) |
so
and
 |
(17) |
Let  , so
, so 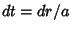 , and
, and
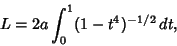 |
(18) |
which, as shown in Lemniscate Function, is given analytically by
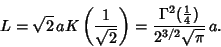 |
(19) |
If 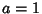 , then
, then
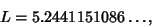 |
(20) |
which is related to Gauss's Constant 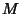 by
by
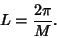 |
(21) |
The quantity  or
or  is called the Lemniscate Constant and plays a role for the lemniscate analogous to
that of
is called the Lemniscate Constant and plays a role for the lemniscate analogous to
that of 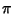 for the Circle.
for the Circle.
The Area of one loop of the lemniscate is
See also Lemniscate Function
References
Ayoub, R. ``The Lemniscate and Fagnano's Contributions to Elliptic Integrals.'' Arch. Hist. Exact Sci. 29, 131-149, 1984.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, 1987.
Gray, A. ``Lemniscates of Bernoulli.'' §3.2 in Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 39-41, 1993.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 120-124, 1972.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 37, 1983.
Lee, X. ``Lemniscate of Bernoulli.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/LemniscateOfBernoulli_dir/lemniscateOfBernoulli.html.
Lockwood, E. H. A Book of Curves. Cambridge, England: Cambridge University Press, 1967.
MacTutor History of Mathematics Archive. ``Lemniscate of Bernoulli.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Lemniscate.html.
Yates, R. C. ``Lemniscate.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 143-147, 1952.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() , the Cartesian equation is
, the Cartesian equation is
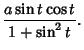
![]() published an article in Acta Eruditorum in 1694 in which he called
this curve the lemniscus (``a pendant ribbon''). Jakob Bernoulli was not aware that the curve he was describing was a
special case of Cassini Ovals which had been described by Cassini
published an article in Acta Eruditorum in 1694 in which he called
this curve the lemniscus (``a pendant ribbon''). Jakob Bernoulli was not aware that the curve he was describing was a
special case of Cassini Ovals which had been described by Cassini ![]() in 1680. The general properties of
the lemniscate were discovered by G. Fagnano in 1750 (MacTutor Archive). Gauss's
in 1680. The general properties of
the lemniscate were discovered by G. Fagnano in 1750 (MacTutor Archive). Gauss's ![]() and
Euler's
and
Euler's ![]() investigations of the Arc Length of the curve led to later work on Elliptic
Functions.
investigations of the Arc Length of the curve led to later work on Elliptic
Functions.
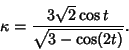
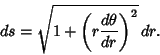



![$\displaystyle {\textstyle{1\over 2}}\int r^2\,d\theta = {\textstyle{1\over 2}}a...
...(2\theta)\,d\theta = {\textstyle{1\over 4}}a^2 [\sin(2\theta)]^{\pi/4}_{-\pi/4}$](l1_1513.gif)