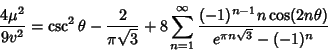The lemniscate functions arise in rectifying the Arc Length of the Lemniscate. The lemniscate functions
were first studied by Jakob Bernoulli  and G. Fagnano. A historical account is given by
Ayoub (1984), and an extensive discussion by Siegel (1969). The lemniscate functions were the first functions defined by
inversion of an integral, which was first done by Gauß.
and G. Fagnano. A historical account is given by
Ayoub (1984), and an extensive discussion by Siegel (1969). The lemniscate functions were the first functions defined by
inversion of an integral, which was first done by Gauß. 
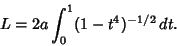 |
(1) |
Define the functions
where
 |
(4) |
and write
There is an identity connecting 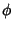 and
and 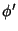 since
since
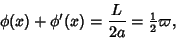 |
(7) |
so
 |
(8) |
These functions can be written in terms of Jacobi Elliptic Functions,
![\begin{displaymath}
u=\int_0^{{\rm sd} (u,k)} [(1-k'^2y^2)(1+k^2y^2)]^{-1/2}\,dy.
\end{displaymath}](l1_1530.gif) |
(9) |
Now, if
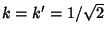 , then
, then
Let
 so
so
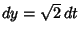 ,
,
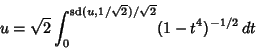 |
(11) |
 |
(12) |
 |
(13) |
and
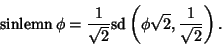 |
(14) |
Similarly,
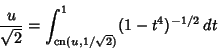 |
(16) |
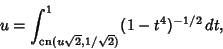 |
(17) |
and
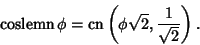 |
(18) |
We know
 |
(19) |
But it is true that
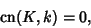 |
(20) |
so
 |
(21) |
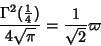 |
(22) |
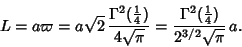 |
(23) |
By expanding
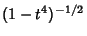 in a Binomial Series and integrating term by term, the arcsinlemn function can be
written
in a Binomial Series and integrating term by term, the arcsinlemn function can be
written
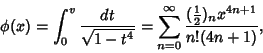 |
(24) |
where 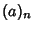 is the Rising Factorial (Berndt 1994). Ramanujan
is the Rising Factorial (Berndt 1994). Ramanujan  gave the following inversion
Formula for
gave the following inversion
Formula for  . If
. If
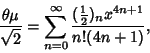 |
(25) |
where
 |
(26) |
is the constant obtained by letting 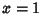 and
and 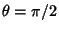 , and
, and
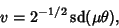 |
(27) |
then
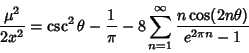 |
(28) |
(Berndt 1994). Ramanujan  also showed that if
also showed that if
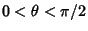 , then
, then
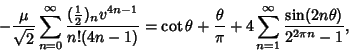 |
(29) |
 |
(30) |
![\begin{displaymath}
{\textstyle{1\over 2}}\tan^{-1} v=\sum_{n=0}^\infty {\sin[(2n+1)\theta]\over (2n+1)\cosh[{\textstyle{1\over 2}}(2n+1)\pi]},
\end{displaymath}](l1_1563.gif) |
(31) |
![\begin{displaymath}
{\textstyle{1\over 4}}\cos^{-1}(v^2)=\sum_{n=0}^\infty {(-1)...
...+1)\theta]\over (2n+1)\cosh[{\textstyle{1\over 2}}(2n+1)\pi]},
\end{displaymath}](l1_1564.gif) |
(32) |
and
![\begin{displaymath}
{\sqrt{2}\over 4\mu}\sum_{n=0}^\infty {2^{2n}(n!)^2\over (2n...
...+1)\theta]\over(2n+1)^2\cosh[{\textstyle{1\over 2}}(2n+1)\pi]}
\end{displaymath}](l1_1565.gif) |
(33) |
(Berndt 1994).
A generalized version of the lemniscate function can be defined by
letting
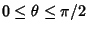 and
and  . Write
. Write
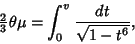 |
(34) |
where 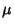 is the constant obtained by setting
is the constant obtained by setting 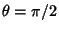 and
and 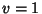 . Then
. Then
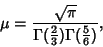 |
(35) |
and Ramanujan  showed
showed
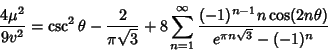 |
(36) |
(Berndt 1994).
See also Hyperbolic Lemniscate Function
References
Ayoub, R. ``The Lemniscate and Fagnano's Contributions to Elliptic Integrals.'' Arch. Hist. Exact Sci.
29, 131-149, 1984.
Berndt, B. C. Ramanujan's Notebooks, Part IV.
New York: Springer-Verlag, pp. 245, and 247-255, 258-260, 1994.
Siegel, C. L. Topics in Complex Function Theory, Vol. 1. New York: Wiley, 1969.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() and G. Fagnano. A historical account is given by
Ayoub (1984), and an extensive discussion by Siegel (1969). The lemniscate functions were the first functions defined by
inversion of an integral, which was first done by Gauß.
and G. Fagnano. A historical account is given by
Ayoub (1984), and an extensive discussion by Siegel (1969). The lemniscate functions were the first functions defined by
inversion of an integral, which was first done by Gauß. ![]()
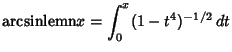
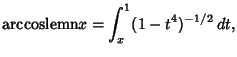
![$\displaystyle \int_0^{{\rm sd}(u,1/\sqrt{2})} [(1-{\textstyle{1\over 2}}y^2)(1+{\textstyle{1\over 2}}y^2)]^{-1/2}\,dy$](l1_1532.gif)

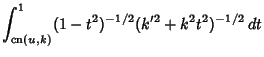

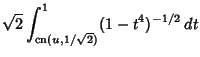
![]() in a Binomial Series and integrating term by term, the arcsinlemn function can be
written
in a Binomial Series and integrating term by term, the arcsinlemn function can be
written
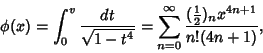
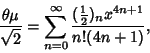
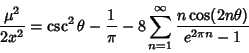
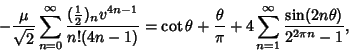

![\begin{displaymath}
{\textstyle{1\over 2}}\tan^{-1} v=\sum_{n=0}^\infty {\sin[(2n+1)\theta]\over (2n+1)\cosh[{\textstyle{1\over 2}}(2n+1)\pi]},
\end{displaymath}](l1_1563.gif)
![\begin{displaymath}
{\textstyle{1\over 4}}\cos^{-1}(v^2)=\sum_{n=0}^\infty {(-1)...
...+1)\theta]\over (2n+1)\cosh[{\textstyle{1\over 2}}(2n+1)\pi]},
\end{displaymath}](l1_1564.gif)
![\begin{displaymath}
{\sqrt{2}\over 4\mu}\sum_{n=0}^\infty {2^{2n}(n!)^2\over (2n...
...+1)\theta]\over(2n+1)^2\cosh[{\textstyle{1\over 2}}(2n+1)\pi]}
\end{displaymath}](l1_1565.gif)
![]() and
and ![]() . Write
. Write