|
|
|
Let ![]() be a curve and let
be a curve and let ![]() be a fixed point. Let
be a fixed point. Let ![]() be on
be on ![]() and let
and let ![]() be the Curvature Center at
be the Curvature Center at ![]() . Let
. Let
![]() be the point with
be the point with ![]() a line segment Parallel and of equal length to
a line segment Parallel and of equal length to ![]() . Then the curve traced by
. Then the curve traced by ![]() is the radial curve of
is the radial curve of ![]() . It was studied by Robert Tucker in 1864. The parametric equations of a curve
. It was studied by Robert Tucker in 1864. The parametric equations of a curve ![]() with
Radial Point
with
Radial Point ![]() are
are
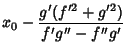 |
|||
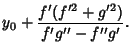 |
| Curve | Radial Curve |
| Astroid | Quadrifolium |
| Catenary | Kampyle of Eudoxus |
| Cycloid | Circle |
| Deltoid | Trifolium |
| Logarithmic Spiral | Logarithmic Spiral |
| Tractrix | Kappa Curve |
References
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 40 and 202, 1972.
Yates, R. C. ``Radial Curves.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 172-174, 1952.