Tractrix

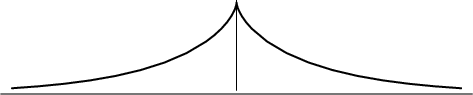
$\begin{figure}\begin{center}\BoxedEPSF{Tractrix.epsf scaled 810}\end{center}\end{figure}$

The tractrix is the Catenary Involute described by a point initially on the vertex. It is sometimes called the Tractory or Equitangential Curve. The tractrix was first studied by Huygens in 1692, who gave it the name ``tractrix.'' Later, Leibniz, Johann Bernoulli, and others studied the curve.

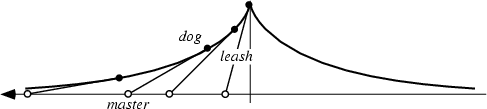
$\begin{figure}\begin{center}\BoxedEPSF{TractrixDiagram.epsf scaled 800}\end{center}\end{figure}$

The tractrix arises from the following problem posed to Leibniz: What is the path of an object starting off with a vertical offset when it is dragged along by a string of constant length being pulled along a straight horizontal line? By associating the object with a dog, the string with a leash, and the pull along a horizontal line with the dog's master, the curve has the descriptive name Hundkurve (hound curve) in German. Leibniz found the curve using the fact that the axis is an asymptote to the tractrix (MacTutor Archive).

In Cartesian Coordinates the tractrix has equation

$\begin{displaymath} x=a\mathop{\rm sech}\nolimits ^{-1}\left({y\over a}\right)-\sqrt{a^2-y^2}. \end{displaymath}$

(1)

One parametric form is

$\displaystyle x(t)$	$\textstyle =$	$\displaystyle a(t-\tanh t)$	(2)
$\displaystyle y(t)$	$\textstyle =$	$\displaystyle a\mathop{\rm sech}\nolimits t.$	(3)

$\begin{figure}\begin{center}\BoxedEPSF{TractrixInfo.epsf scaled 740}\end{center}\end{figure}$

The Arc Length, Curvature, and Tangential Angle are

$\displaystyle s(t)$	$\textstyle =$	$\displaystyle \ln(\cosh t)$	(4)
$\displaystyle \kappa(t)$	$\textstyle =$	$\displaystyle \mathop{\rm csch}\nolimits t$	(5)
$\displaystyle \phi(t)$	$\textstyle =$	$\displaystyle 2\tan^{-1}[\tanh({\textstyle{1\over 2}}t)].$	(6)

A second parametric form in terms of the Angle $\theta$ of the straight line tangent to the tractrix is

$\displaystyle x$	$\textstyle =$	$\displaystyle a\{\ln[\tan({\textstyle{1\over 2}}\theta)]+\cos\theta\}$	(7)
$\displaystyle y$	$\textstyle =$	$\displaystyle a\sin\theta$	(8)

(Gray 1993). This parameterization has Curvature

$\begin{displaymath} \kappa(\theta)=\vert\tan\theta\vert. \end{displaymath}$

(9)

A parameterization which traverses the tractrix with constant speed

is given by

$\displaystyle x(t)$	$\textstyle =$	$\displaystyle \left\{\begin{array}{ll} ae^{-v/a} & \mbox{for $v\in [0,\infty)$}\\ ae^{v/a} & \mbox{for $v\in (-\infty, 0]$}\end{array}\right.$	(10)
$\displaystyle y(t)$	$\textstyle =$	$\displaystyle \left\{\begin{array}{ll} a[\tanh^{-1}(\sqrt{1-e^{-2v/a}}\,)-\sqrt... ...}] & \mbox{}\\ \quad {\rm for\ }v\in (-\infty, 0]. & \mbox{}\end{array}\right.$
			(11)

When a tractrix is rotated around its asymptote, a Pseudosphere results. This is a surface of constant Negative Curvature. For a tractrix, the length of a Tangent from its point of contact to an asymptote is constant. The Area between the tractrix and its asymptote is finite.

References

Geometry Center. ``The Tractrix.'' http://www.geom.umn.edu/zoo/diffgeom/pseudosphere/tractrix.html.

Gray, A. ``The Tractrix'' and ``The Evolute of a Tractrix is a Catenary.'' §3.5 and 5.3 in Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 46-50 and 80-81, 1993.

Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 199-200, 1972.

Lee, X. ``Tractrix.'' http://www.best.com/~xah/SpecialPlaneCurves_dir/Tractrix_dir/tractrix.html.

Lockwood, E. H. ``The Tractrix and Catenary.'' Ch. 13 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 118-124, 1967.

MacTutor History of Mathematics Archive. ``Tractrix.'' http://www-groups.dcs.st-and.ac.uk/~history/Curves/Tractrix.html.

Yates, R. C. ``Tractrix.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 221-224, 1952.