|
|
|
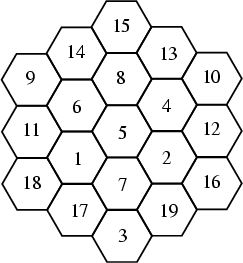
An arrangement of close-packed Hexagons containing the numbers 1, 2, ..., ![]() , where
, where ![]() is the
is the ![]() th Hex Number, such that the numbers along each straight line add up to the same sum. In the above magic
hexagon, each line (those of lengths 3, 4, and 5) adds up to 38. This is the only magic hexagon of the counting numbers for
any size hexagon. It was discovered by C. W. Adams, who worked on the problem from 1910 to 1957.
th Hex Number, such that the numbers along each straight line add up to the same sum. In the above magic
hexagon, each line (those of lengths 3, 4, and 5) adds up to 38. This is the only magic hexagon of the counting numbers for
any size hexagon. It was discovered by C. W. Adams, who worked on the problem from 1910 to 1957.
See also Hex Number, Hexagon, Magic Graph, Magic Square, Talisman Hexagon
References
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT
Artificial Intelligence Laboratory, Memo AIM-239, Item 49, Feb. 1972.
Gardner, M. ``Permutations and Paradoxes in Combinatorial Mathematics.'' Sci. Amer. 209, 112-119, Aug. 1963.
Honsberger, R. Mathematical Gems I. Washington, DC: Math. Assoc. Amer., pp. 69-76, 1973.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 100-101, 1979.