|
|
|
Given a Complete Graph ![]() which is two-colored, the number of forced monochromatic Triangles is at least
which is two-colored, the number of forced monochromatic Triangles is at least
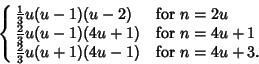
See also Complete Graph, Extremal Graph
References
Goodman, A. W. ``On Sets of Acquaintances and Strangers at Any Party.'' Amer. Math. Monthly 66, 778-783, 1959.
Sloane, N. J. A. Sequence
A014557
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.