|
|
|
A Finite Group of Order ![]() for
for ![]() a Prime is called a
a Prime is called a ![]() -group. Sylow proved
that every Group of this form has a Power-commutator representation on
-group. Sylow proved
that every Group of this form has a Power-commutator representation on ![]() generators defined by
generators defined by
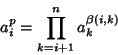 |
(1) |
![\begin{displaymath}[a_j,a_i]=\prod_{k=j+1}^n a_k^{\beta(i,j,k)}
\end{displaymath}](p1_65.gif) |
(2) |
| (3) |
| (4) |
See also Finite Group
References
Higman, G. ``Enumerating
Higman, G. ``Enumerating
![]() -Groups. I. Inequalities.'' Proc. London Math. Soc. 10, 24-30, 1960a.
-Groups. I. Inequalities.'' Proc. London Math. Soc. 10, 24-30, 1960a.
![]() -Groups. II. Problems Whose Solution is PORC.'' Proc. London Math. Soc. 10, 566-582, 1960b.
-Groups. II. Problems Whose Solution is PORC.'' Proc. London Math. Soc. 10, 566-582, 1960b.