|
|
|
Hadamard Matrices
![]() can be constructed using Galois Field GF(
can be constructed using Galois Field GF(![]() ) when
) when ![]() and
and ![]() is Odd. Pick a representation
is Odd. Pick a representation ![]() Relatively Prime to
Relatively Prime to ![]() . Then by coloring white
. Then by coloring white
![]() (where
(where
![]() is the Floor Function) distinct equally spaced Residues mod
is the Floor Function) distinct equally spaced Residues mod ![]() (
(![]() ,
, ![]() ,
,
![]() , ...;
, ...; ![]() ,
, ![]() ,
, ![]() , ...; etc.) in addition to 0, a Hadamard Matrix is obtained if the
Powers of
, ...; etc.) in addition to 0, a Hadamard Matrix is obtained if the
Powers of ![]() (mod
(mod ![]() ) run through
) run through
![]() . For example,
. For example,
![\begin{displaymath}
\left[{\matrix{\infty & \infty & \infty & \infty & \infty & ...
... & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & \infty\cr}}\right]
\end{displaymath}](p1_210.gif)
![]() can be trivially constructed from
can be trivially constructed from
![]() .
.
![]() cannot be built up from smaller
Matrices, so use
cannot be built up from smaller
Matrices, so use
![]() . Only the first form can be used, with
. Only the first form can be used, with
![]() and
and ![]() . We therefore use GF(19), and color 9 Residues plus 0 white.
. We therefore use GF(19), and color 9 Residues plus 0 white.
![]() can be
constructed from
can be
constructed from
![]() .
.
Now consider a more complicated case. For
![]() , the only form having
, the only form having ![]() is the first, so use the
GF(
is the first, so use the
GF(![]() ) field. Take as the modulus the Irreducible Polynomial
) field. Take as the modulus the Irreducible Polynomial ![]() , written 1021. A four-digit number can
always be written using only three digits, since
, written 1021. A four-digit number can
always be written using only three digits, since
![]() and
and
![]() . Now look at the moduli
starting with 10, where each digit is considered separately. Then
. Now look at the moduli
starting with 10, where each digit is considered separately. Then
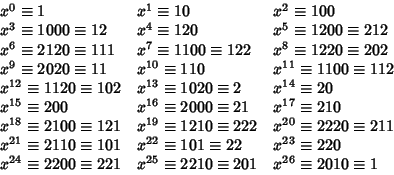
Taking the alternate terms gives white squares as 000, 001, 020, 021, 022, 100, 102, 110, 111, 120, 121, 202, 211, and 221.
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover,
pp. 107-109 and 274, 1987.
Beth, T.; Jungnickel, D.; and Lenz, H. Design Theory, 2nd ed. rev. Cambridge, England: Cambridge University Press, 1998.
Geramita, A. V. Orthogonal Designs: Quadratic Forms and Hadamard Matrices.
New York: Marcel Dekker, 1979.
![]() Kitis, L. ``Paley's Construction of Hadamard Matrices.''
http://www.mathsource.com/cgi-bin/MathSource/Applications/Mathematics/0205-760.
Kitis, L. ``Paley's Construction of Hadamard Matrices.''
http://www.mathsource.com/cgi-bin/MathSource/Applications/Mathematics/0205-760.
|
|
|
© 1996-9 Eric W. Weisstein