|
|
|
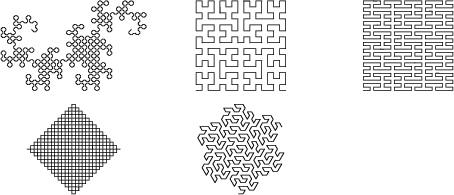
A Space-Filling Function which maps a 1-D Interval into a 2-D area. Plane-filling functions
were thought to be impossible until Hilbert ![]() discovered the Hilbert Curve in 1891.
discovered the Hilbert Curve in 1891.
Plane-filling functions are often (imprecisely) defined to be the ``limit'' of an infinite sequence of specified curves which ``fill'' the Plane without ``Holes,'' hence the more popular term Plane-Filling Curve. The term ``plane-filling function'' is preferable to ``Plane-Filling Curve'' because ``curve'' informally connotes ``Graph'' (i.e., range) of some continuous function, but the Graph of a plane-filling function is a solid patch of 2-space with no evidence of the order in which it was traced (and, for a dense set, retraced). Actually, all that is needed to rigorously define a plane-filling function is an arbitrarily refinable correspondence between contiguous subintervals of the domain and contiguous subareas of the range.
True plane-filling functions are not One-to-One. In fact, because they map closed intervals onto closed areas, they cannot help but overfill, revisiting at least twice a dense subset of the filled area. Thus, every point in the filled area has at least one inverse image.
See also Hilbert Curve, Peano Curve, Peano-Gosper Curve, Sierpinski Curve, Space-Filling Function, Space-Filling Polyhedron
References
Bogomolny, A. ``Plane Filling Curves.''
http://www.cut-the-knot.com/do_you_know/hilbert.html.
Wagon, S. ``A Space-Filling Curve.'' §6.3 in Mathematica in Action. New York: W. H. Freeman, pp. 196-209, 1991.