Find the minimum distance between a point in the plane 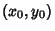 and a quadratic Plane Curve
and a quadratic Plane Curve
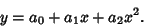 |
(1) |
The square of the distance is
Minimizing the distance squared is the equivalent to minimizing the distance (since 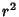 and
and 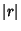 have minima at the
same point), so take
have minima at the
same point), so take
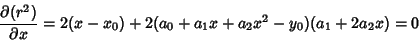 |
(3) |
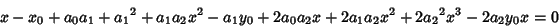 |
(4) |
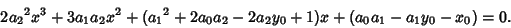 |
(5) |
Minimizing the distance therefore requires solution of a Cubic Equation.
See also Point-Point Distance--1-D, Point-Point Distance--2-D,
Point-Point Distance--3-D
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and a quadratic Plane Curve
and a quadratic Plane Curve