|
|
|
Given a unit Line Segment ![]() , pick two points at random on it. Call the first point
, pick two points at random on it. Call the first point ![]() and the second
point
and the second
point ![]() . Find the distribution of distances
. Find the distribution of distances ![]() between points. The probability of the points being a
(Positive) distance
between points. The probability of the points being a
(Positive) distance ![]() apart (i.e., without regard to ordering) is given by
apart (i.e., without regard to ordering) is given by
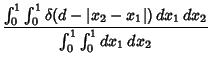 |
|||
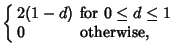 |
(1) |
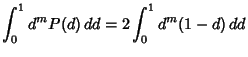 |
|||
![$\displaystyle 2\left[{{d^{m+1}\over m+1}-{d^{m+2}\over m+2}}\right]_0^1$](p2_833.gif) |
|||
![$\displaystyle 2\left({{1\over m+1}-{1\over m+2}}\right)=2\left[{(m+2)-(m+1)\over (m+1)(m+2)}\right]$](p2_834.gif) |
|||
 |
(2) |
| (3) | |||
| (4) | |||
| (5) | |||
| (6) |
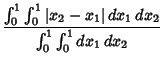 |
|||
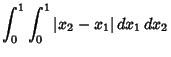 |
|||
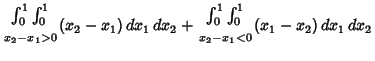 |
|||
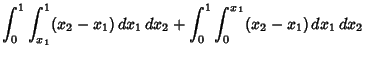 |
|||
![$\displaystyle \int_0^1 \left[{{\textstyle{1\over 2}}{x_2}^2-x_1x_2}\right]_{x_1...
...dx_1+\int_0^1 \left[{x_1x_2-{\textstyle{1\over 2}}{x_2}^2}\right]^{x_1}_0\,dx_1$](p2_849.gif) |
|||
![$\displaystyle \int_0^1 \left[{({\textstyle{1\over 2}}-x_1)-({\textstyle{1\over ...
..._1+ \int_0^1 \left[{({x_1}^2-{\textstyle{1\over 2}}{x_1}^2)-(0-0)}\right]\,dx_1$](p2_850.gif) |
|||
![$\displaystyle \int_0^1 ({\textstyle{1\over 2}}-x_1+{x_1}^2)\,dx_1 = [{\textstyle{1\over 2}}x_1-{\textstyle{1\over 2}}{x_1}^2+{\textstyle{1\over 3}}{x_1}^3]^1_0$](p2_851.gif) |
|||
| (7) | |||
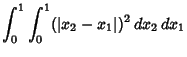 |
|||
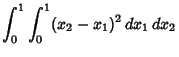 |
|||
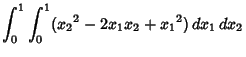 |
|||
![$\displaystyle \int_0^1 [{\textstyle{1\over 3}}{x_2}^3-x_1{x_2}^2+{x_1}^2x_2]^1_0\,dx_1$](p2_856.gif) |
|||
![$\displaystyle \int_0^1 ({\textstyle{1\over 3}}-x_1+{x_1}^2)\,dx_1 = [{\textstyle{1\over 3}}{x_1}^3-{\textstyle{1\over 2}}{x_1}^2+{\textstyle{1\over 3}}x_1]^1_0$](p2_857.gif) |
|||
| (8) |
| (9) | |||
| (10) | |||
| (11) |
| (12) | |||
| (13) | |||
| (14) | |||
| (15) |
See also Point-Point Distance--2-D, Point-Point Distance--3-D, Point-Quadratic Distance, Tetrahedron Inscribing, Triangle Inscribing in a Circle
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 930-931, 1985.
Benedict, B. Using Norton Utilities for the Macintosh. Indianapolis, IN: Que, pp. B-8-B-9, 1995.
|
|
|
© 1996-9 Eric W. Weisstein