|
|
|
Pick four points at random on the surface of a unit Sphere. Find the distribution of possible volumes of
(nonregular) Tetrahedra. Without loss of generality, the first point can be chosen as (1, 0, 0).
Designate the other points ![]() ,
, ![]() , and
, and ![]() . Then the distances from the first Vertex are
. Then the distances from the first Vertex are
![$\displaystyle \left[\begin{array}{c}\cos\theta_1-1\\ \sin\theta_1\\ 0\end{array}\right]$](t_476.gif) |
(1) | ||
![$\displaystyle \left[\begin{array}{c}\cos\theta_2\sin\phi_2-1\\ \sin\theta_2\sin\phi_2\\ \cos\phi_2\end{array}\right]$](t_478.gif) |
(2) | ||
![$\displaystyle \left[\begin{array}{c}\cos\theta_3\sin\phi_3-1\\ \sin\theta_3\sin\phi_3\\ \cos\phi_3\end{array}\right].$](t_480.gif) |
(3) |
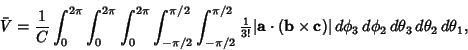 |
(4) |
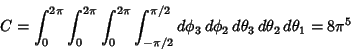 |
(5) |
|
|
|
|
|
|
|
|
|
|
|
(6) |
| (7) | |||
| (8) | |||
| (9) |
See also Point-Point Distance--1-D, Triangle Inscribing in a Circle, Triangle Inscribing in an Ellipse
References
Buchta, C. ``A Note on the Volume of a Random Polytope in a Tetrahedron.'' Ill. J. Math. 30, 653-659, 1986.