A cubic equation is a Polynomial equation of degree three. Given a general cubic equation
 |
(1) |
(the Coefficient  of
of  may be taken as 1 without loss of generality by dividing the entire equation through by
may be taken as 1 without loss of generality by dividing the entire equation through by
 ), first attempt to eliminate the
), first attempt to eliminate the  term by making a substitution of the form
term by making a substitution of the form
 |
(2) |
Then
The 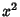 is eliminated by letting
is eliminated by letting 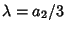 , so
, so
 |
(6) |
Then
so equation (1) becomes
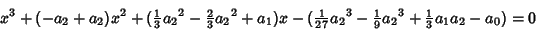 |
(10) |
 |
(11) |
 |
(12) |
Defining
then allows (12) to be written in the standard form
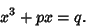 |
(15) |
The simplest way to proceed is to make Vieta's Substitution
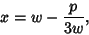 |
(16) |
which reduces the cubic to the equation
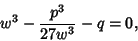 |
(17) |
which is easily turned into a Quadratic Equation in  by multiplying through by
by multiplying through by  to obtain
to obtain
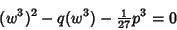 |
(18) |
(Birkhoff and Mac Lane 1965, p. 106). The result from the Quadratic Equation is
where 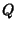 and
and 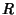 are sometimes more useful to deal with than are
are sometimes more useful to deal with than are 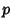 and
and 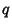 . There are therefore six solutions for
. There are therefore six solutions for
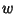 (two corresponding to each sign for each Root of
(two corresponding to each sign for each Root of  ). Plugging
). Plugging 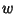 back in to (17) gives three pairs of
solutions, but each pair is equal, so there are three solutions to the cubic equation.
back in to (17) gives three pairs of
solutions, but each pair is equal, so there are three solutions to the cubic equation.
Equation (12) may also be explicitly factored by attempting to pull out a term of the form  from the cubic
equation, leaving behind a quadratic equation which can then be factored using the Quadratic Formula. This process
is equivalent to making Vieta's substitution, but does a slightly better job of motivating Vieta's ``magic''
substitution, and also at producing the explicit formulas for the solutions. First, define the intermediate variables
from the cubic
equation, leaving behind a quadratic equation which can then be factored using the Quadratic Formula. This process
is equivalent to making Vieta's substitution, but does a slightly better job of motivating Vieta's ``magic''
substitution, and also at producing the explicit formulas for the solutions. First, define the intermediate variables
(which are identical to 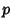 and
and 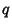 up to a constant factor). The general cubic equation (12) then becomes
up to a constant factor). The general cubic equation (12) then becomes
 |
(22) |
Let 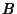 and
and 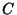 be, for the moment, arbitrary constants. An identity satisfied by Perfect Cubic
equations is that
be, for the moment, arbitrary constants. An identity satisfied by Perfect Cubic
equations is that
 |
(23) |
The general cubic would therefore be directly factorable if it did not have an 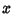 term (i.e., if
term (i.e., if  ). However, since
in general
). However, since
in general 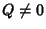 , add a multiple of
, add a multiple of  --say
--say  --to both sides of (23) to give the slightly messy
identity
--to both sides of (23) to give the slightly messy
identity
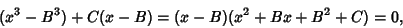 |
(24) |
which, after regrouping terms, is
![\begin{displaymath}
x^3+Cx-(B^3+BC)=(x-B)[x^2+Bx+(B^2+C)]=0.
\end{displaymath}](c4_176.gif) |
(25) |
We would now like to match the Coefficients 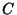 and
and 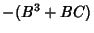 with those of equation (22), so we must have
with those of equation (22), so we must have
 |
(26) |
 |
(27) |
Plugging the former into the latter then gives
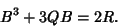 |
(28) |
Therefore, if we can find a value of 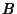 satisfying the above identity, we have factored a linear term from the cubic,
thus reducing it to a Quadratic Equation. The trial solution accomplishing this miracle turns out to be the symmetrical expression
satisfying the above identity, we have factored a linear term from the cubic,
thus reducing it to a Quadratic Equation. The trial solution accomplishing this miracle turns out to be the symmetrical expression
![\begin{displaymath}
B=[R+\sqrt{Q^3+R^2}\,]^{1/3}+[R-\sqrt{Q^3+R^2}\,]^{1/3}.
\end{displaymath}](c4_181.gif) |
(29) |
Taking the second and third Powers of 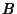 gives
gives
Plugging 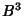 and
and 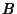 into the left side of (28) gives
into the left side of (28) gives
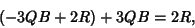 |
(32) |
so we have indeed found the factor  of (22), and we need now only factor the quadratic part. Plugging
of (22), and we need now only factor the quadratic part. Plugging 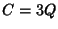 into the quadratic part of (25) and solving the resulting
into the quadratic part of (25) and solving the resulting
 |
(33) |
then gives the solutions
These can be simplified by defining
so that the solutions to the quadratic part can be written
 |
(37) |
Defining
where  is the Discriminant (which is defined slightly differently, including
the opposite Sign, by Birkhoff and Mac Lane 1965) then gives very simple expressions for
is the Discriminant (which is defined slightly differently, including
the opposite Sign, by Birkhoff and Mac Lane 1965) then gives very simple expressions for 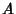 and
and 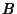 , namely
, namely
Therefore, at last, the Roots of the original equation in 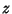 are then given by
are then given by
with  the Coefficient of
the Coefficient of  in the original equation, and
in the original equation, and 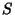 and
and 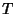 as defined above. These three equations
giving the three Roots of the cubic equation are sometimes known as Cardano's Formula. Note that if the equation
is in the standard form of Vieta
as defined above. These three equations
giving the three Roots of the cubic equation are sometimes known as Cardano's Formula. Note that if the equation
is in the standard form of Vieta
 |
(46) |
in the variable 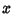 , then
, then  ,
,  , and
, and 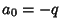 , and the intermediate variables have the simple form
(c.f. Beyer 1987)
, and the intermediate variables have the simple form
(c.f. Beyer 1987)
The equation for  in Cardano's Formula does not have an
in Cardano's Formula does not have an  appearing in it explicitly while
appearing in it explicitly while 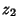 and
and 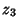 do,
but this does not say anything about the number of Real and Complex Roots
(since
do,
but this does not say anything about the number of Real and Complex Roots
(since 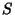 and
and 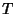 are themselves, in general, Complex). However, determining which
Roots are Real and which are Complex can be accomplished by
noting that if the Discriminant
are themselves, in general, Complex). However, determining which
Roots are Real and which are Complex can be accomplished by
noting that if the Discriminant  , one Root is Real
and two are Complex Conjugates; if
, one Root is Real
and two are Complex Conjugates; if  , all Roots are Real and at least two are equal; and if
, all Roots are Real and at least two are equal; and if 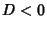 , all Roots are Real and unequal. If
, all Roots are Real and unequal. If
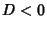 , define
, define
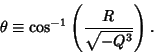 |
(50) |
Then the Real solutions are of the form
This procedure can be generalized to find the Real Roots for any equation in the standard form
(46) by using the identity
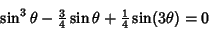 |
(54) |
(Dickson 1914) and setting
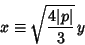 |
(55) |
(Birkhoff and Mac Lane 1965, pp. 90-91), then
 |
(56) |
 |
(57) |
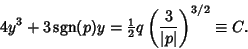 |
(58) |
If  , then use
, then use
 |
(59) |
to obtain
 |
(60) |
If 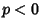 and
and 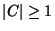 , use
, use
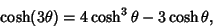 |
(61) |
and if 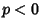 and
and  , use
, use
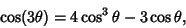 |
(62) |
to obtain
![\begin{displaymath}
y=\cases{
\cosh({\textstyle{1\over 3}}\cosh^{-1} C) & for $...
...{-1} C) \hbox{\ [three solutions]} & for
$\vert C\vert<1$.\cr}
\end{displaymath}](c4_259.gif) |
(63) |
The solutions to the original equation are then
 |
(64) |
An alternate approach to solving the cubic equation is to use Lagrange Resolvents.
Let
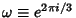 , define
, define
where  are the Roots of
are the Roots of
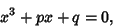 |
(68) |
and consider the equation
![\begin{displaymath}[x-(u_1+u_2)][x-(\omega u_1+\omega^2u_2)][x-(\omega^2u_1+\omega u_2)]=0,
\end{displaymath}](c4_270.gif) |
(69) |
where  and
and  are Complex Numbers. The
Roots are then
are Complex Numbers. The
Roots are then
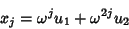 |
(70) |
for  , 1, 2. Multiplying through gives
, 1, 2. Multiplying through gives
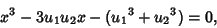 |
(71) |
or
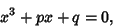 |
(72) |
where
The solutions satisfy Newton's Identities
In standard form,  ,
,  , and
, and 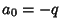 , so we have the identities
, so we have the identities
Some curious identities involving the roots of a cubic equation due to Ramanujan  are given by Berndt (1994).
are given by Berndt (1994).
See also Quadratic Equation, Quartic Equation, Quintic Equation, Sextic Equation
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 17, 1972.
Berger, M. §16.4.1-16.4.11.1 in Geometry I. New York: Springer-Verlag, 1994.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 22-23, 1994.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 9-11, 1987.
Birkhoff, G. and Mac Lane, S. A Survey of Modern Algebra, 3rd ed. New York: Macmillan, pp. 90-91,
106-107, and 414-417, 1965.
Dickson, L. E. ``A New Solution of the Cubic Equation.'' Amer. Math. Monthly 5, 38-39, 1898.
Dickson, L. E. Elementary Theory of Equations. New York: Wiley, pp. 36-37, 1914.
Dunham, W. ``Cardano and the Solution of the Cubic.'' Ch. 6 in
Journey Through Genius: The Great Theorems of Mathematics.
New York: Wiley, pp. 133-154, 1990.
Ehrlich, G. §4.16 in Fundamental Concepts of Abstract Algebra. Boston, MA: PWS-Kent, 1991.
Jones, J. ``Omar Khayyám and a Geometric Solution of the Cubic.''
http://jwilson.coe.uga.edu/emt669/Student.Folders/Jones.June/omar/omarpaper.html.
Kennedy, E. C. ``A Note on the Roots of a Cubic.'' Amer. Math. Monthly 40, 411-412, 1933.
King, R. B. Beyond the Quartic Equation. Boston, MA: Birkhäuser, 1996.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Quadratic and Cubic Equations.'' §5.6 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 178-180, 1992.
Spanier, J. and Oldham, K. B. ``The Cubic Function  and Higher Polynomials.''
Ch. 17 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 131-147, 1987.
and Higher Polynomials.''
Ch. 17 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 131-147, 1987.
van der Waerden, B. L. §64 in Algebra. New York: Frederick Ungar, 1970.
© 1996-9 Eric W. Weisstein
1999-05-25



![]() from the cubic
equation, leaving behind a quadratic equation which can then be factored using the Quadratic Formula. This process
is equivalent to making Vieta's substitution, but does a slightly better job of motivating Vieta's ``magic''
substitution, and also at producing the explicit formulas for the solutions. First, define the intermediate variables
from the cubic
equation, leaving behind a quadratic equation which can then be factored using the Quadratic Formula. This process
is equivalent to making Vieta's substitution, but does a slightly better job of motivating Vieta's ``magic''
substitution, and also at producing the explicit formulas for the solutions. First, define the intermediate variables
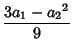
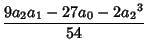
![$\displaystyle \times\left[{\left({R+\sqrt{Q^3+R^2}}\right)^{1/3}+\left({R-\sqrt{Q^3-R^2}}\right)^{1/3}}\right]$](c4_193.gif)

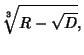

![]() in Cardano's Formula does not have an
in Cardano's Formula does not have an ![]() appearing in it explicitly while
appearing in it explicitly while ![]() and
and ![]() do,
but this does not say anything about the number of Real and Complex Roots
(since
do,
but this does not say anything about the number of Real and Complex Roots
(since ![]() and
and ![]() are themselves, in general, Complex). However, determining which
Roots are Real and which are Complex can be accomplished by
noting that if the Discriminant
are themselves, in general, Complex). However, determining which
Roots are Real and which are Complex can be accomplished by
noting that if the Discriminant ![]() , one Root is Real
and two are Complex Conjugates; if
, one Root is Real
and two are Complex Conjugates; if ![]() , all Roots are Real and at least two are equal; and if
, all Roots are Real and at least two are equal; and if ![]() , all Roots are Real and unequal. If
, all Roots are Real and unequal. If
![]() , define
, define
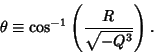
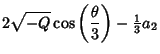

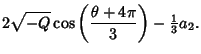
![\begin{displaymath}
y=\cases{
\cosh({\textstyle{1\over 3}}\cosh^{-1} C) & for $...
...{-1} C) \hbox{\ [three solutions]} & for
$\vert C\vert<1$.\cr}
\end{displaymath}](c4_259.gif)
![]() , define
, define

![]() are given by Berndt (1994).
are given by Berndt (1994).
![]() and Higher Polynomials.''
Ch. 17 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 131-147, 1987.
and Higher Polynomials.''
Ch. 17 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 131-147, 1987.