|
|
|
A cubic curve is an Algebraic Curve of degree 3. An algebraic curve over a Field ![]() is an equation
is an equation ![]() ,
where
,
where ![]() is a Polynomial in
is a Polynomial in ![]() and
and ![]() with Coefficients in
with Coefficients in ![]() , and the degree of
, and the degree of ![]() is
the Maximum degree of each of its terms (Monomials).
is
the Maximum degree of each of its terms (Monomials).
Newton ![]() showed that all cubics can be generated by the projection of the five divergent cubic parabolas. Newton's
classification of cubic curves appeared in the chapter ``Curves'' in Lexicon Technicum by John Harris published in London
in 1710. Newton also classified all cubics into 72 types, missing six of them. In addition, he showed that any cubic can be
obtained by a suitable projection of the Elliptic Curve
showed that all cubics can be generated by the projection of the five divergent cubic parabolas. Newton's
classification of cubic curves appeared in the chapter ``Curves'' in Lexicon Technicum by John Harris published in London
in 1710. Newton also classified all cubics into 72 types, missing six of them. In addition, he showed that any cubic can be
obtained by a suitable projection of the Elliptic Curve
| (1) |
| (2) |
| (3) |
| (4) |
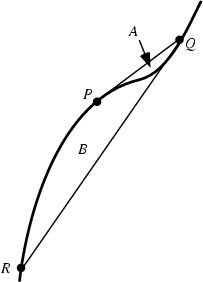
Pick a point ![]() , and draw the tangent to the curve at
, and draw the tangent to the curve at ![]() . Call the point where this tangent intersects the curve
. Call the point where this tangent intersects the curve ![]() .
Draw another tangent and call the point of intersection with the curve
.
Draw another tangent and call the point of intersection with the curve ![]() . Every curve of third degree has the property
that, with the areas in the above labeled figure,
. Every curve of third degree has the property
that, with the areas in the above labeled figure,
| (5) |
See also Cayley-Bacharach Theorem, Cubic Equation
References
Honsberger, R. More Mathematical Morsels. Washington, DC: Math. Assoc. Amer., pp. 114-118, 1991.
Newton, I. Mathematical Works, Vol. 2. New York: Johnson Reprint Corp., pp. 135-161, 1967.
Wall, C. T. C. ``Affine Cubic Functions III.'' Math. Proc. Cambridge Phil. Soc. 87, 1-14, 1980.
Westfall, R. S. Never at Rest: A Biography of Isaac Newton. New York: Cambridge University Press, 1988.
Yates, R. C. ``Cubic Parabola.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 56-59, 1952.
|
|
|
© 1996-9 Eric W. Weisstein