Birkhoff, G. and Mac Lane, S. A Survey of Modern Algebra, 3rd ed. New York: Macmillan, pp. 418-421, 1965.
Chowla, S. ``On Quintic Equations Soluble by Radicals.'' Math. Student 13, 84, 1945.
Cockle, J. ``Sketch of a Theory of Transcendental Roots.'' Phil. Mag. 20, 145-148, 1860.
Cockle, J. `` On Transcendental and Algebraic Solution--Supplemental Paper.'' Phil. Mag. 13, 135-139, 1862.
Davis, H. T. Introduction to Nonlinear Differential and Integral Equations. New York: Dover, p. 172, 1960.
Dummit, D. S. ``Solving Solvable Quintics.'' Math. Comput. 57, 387-401, 1991.
Glashan, J. C. ``Notes on the Quintic.'' Amer. J. Math. 8, 178-179, 1885.
Harley, R. ``On the Solution of the Transcendental Solution of Algebraic Equations.''
Quart. J. Pure Appl. Math. 5, 337-361, 1862.
Hermite, C. ``Sulla risoluzione delle equazioni del quinto grado.'' Annali di math. pura ed appl. 1, 256-259, 1858.
King, R. B. Beyond the Quartic Equation. Boston, MA: Birkhäuser, 1996.
King, R. B. and Cranfield, E. R. ``An Algorithm for Calculating the Roots of a General Quintic Equation
from Its Coefficients.'' J. Math. Phys. 32, 823-825, 1991.
Rosen, M. I. ``Niels Hendrik Abel and Equations of the Fifth Degree.'' Amer. Math. Monthly 102, 495-505, 1995.
Shurman, J. Geometry of the Quintic. New York: Wiley, 1997.
Spearman, B. K. and Williams, K. S. ``Characterization of Solvable Quintics 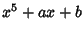 .''
Amer. Math. Monthly 101, 986-992, 1994.
.''
Amer. Math. Monthly 101, 986-992, 1994.
Young, G. P. ``Solution of Solvable Irreducible Quintic Equations, Without the Aid of a Resolvent Sextic.'' Amer. J. Math. 7, 170-177,
1885.
![]() and Galois.
and Galois. ![]()
![]() reduced the general quintic to
reduced the general quintic to
![\begin{displaymath}
\prod_{j=0}^4 [x-(\omega^ju_1+\omega^{4j}u_2)]=0,
\end{displaymath}](q_858.gif)
![\begin{displaymath}
\prod_{j=0}^4 [x-(\omega^ju_1+\omega^{2j}u_2+\omega^{3j}u_3+\omega^{4j}u_4)]=0.
\end{displaymath}](q_861.gif)
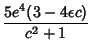
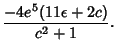
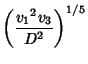
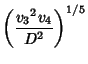

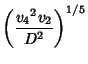
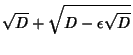
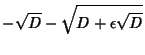

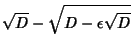
![$\displaystyle \tan\left[{{\textstyle{1\over 4}}\sin^{-1}\left({16\over 25 \sqrt{5}\,\rho^2}\right)}\right]$](q_910.gif)
![$\displaystyle \left\{\begin{array}{ll} -\mathop{\rm sgn}\nolimits (\Im[\rho]) &...
...{\rm sgn}\nolimits (\Re[\rho]) & \mbox{for $\Re[\rho]\not=0$}\end{array}\right.$](q_912.gif)
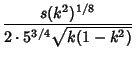
![]() used a Tschirnhausen Transformation to reduce the general quintic to the form
used a Tschirnhausen Transformation to reduce the general quintic to the form
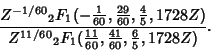
![]() ,
, ![]() , and
, and ![]() missing have the following form
missing have the following form
![]() .''
Amer. Math. Monthly 101, 986-992, 1994.
.''
Amer. Math. Monthly 101, 986-992, 1994.