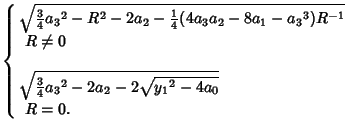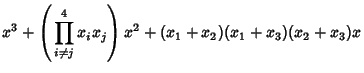A general quartic equation (also called a Biquadratic Equation) is a fourth-order Polynomial of the form
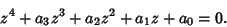 |
(1) |
The Roots of this equation satisfy Newton's Relations:
where the denominators on the right side are all 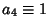 .
.
Ferrari was the first to develop an algebraic technique for solving the general quartic.
He applied his technique (which was stolen and published by Cardano) to the equation
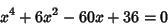 |
(6) |
(Smith 1994, p. 207).
The 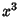 term can be eliminated from the general quartic (1) by making a substitution
of the form
term can be eliminated from the general quartic (1) by making a substitution
of the form
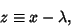 |
(7) |
so
Letting 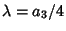 so
so
 |
(9) |
then gives
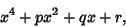 |
(10) |
where
Adding and subtracting 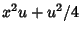 to (10) gives
to (10) gives
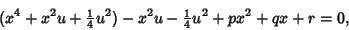 |
(14) |
which can be rewritten
![\begin{displaymath}
(x^2+{\textstyle{1\over 2}}u)^2-[(u-p)x^2-qx+({\textstyle{1\over 4}}u^2-r)]=0
\end{displaymath}](q_677.gif) |
(15) |
(Birkhoff and Mac Lane 1965). The first term is a perfect square 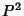 , and the second term is a perfect square
, and the second term is a perfect square 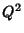 for those
for those 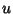 such that
such that
 |
(16) |
This is the resolvent Cubic, and plugging a solution 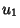 back in gives
back in gives
 |
(17) |
so (15) becomes
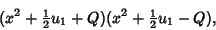 |
(18) |
where
Let 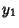 be a Real Root of the resolvent Cubic Equation
be a Real Root of the resolvent Cubic Equation
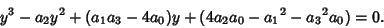 |
(22) |
The four Roots are then given by the Roots of the equation
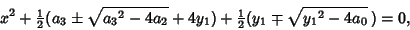 |
(23) |
which are
where
Another approach to solving the quartic (10) defines
where use has been made of
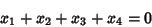 |
(34) |
(which follows since 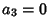 ), and
), and
Comparing with
gives
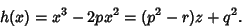 |
(40) |
Solving this Cubic Equation gives 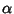 ,
, 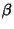 , and
, and 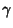 , which can then be solved for the roots of
the quartic
, which can then be solved for the roots of
the quartic 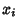 (Faucette 1996).
(Faucette 1996).
See also Cubic Equation, Discriminant (Polynomial), Quintic Equation
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 17-18, 1972.
Berger, M. §16.4.1-16.4.11.1 in Geometry I. New York: Springer-Verlag, 1987.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 12, 1987.
Birkhoff, G. and Mac Lane, S. A Survey of Modern Algebra, 3rd ed. New York: Macmillan, pp. 107-108, 1965.
Ehrlich, G. §4.16 in Fundamental Concepts of Abstract Algebra. Boston, MA: PWS-Kent, 1991.
Faucette, W. M. ``A Geometric Interpretation of the Solution of the General Quartic Polynomial.''
Amer. Math. Monthly 103, 51-57, 1996.
Smith, D. E. A Source Book in Mathematics. New York: Dover, 1994.
van der Waerden, B. L. §64 in Algebra, Vol. 1. New York: Springer-Verlag, 1993.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() term can be eliminated from the general quartic (1) by making a substitution
of the form
term can be eliminated from the general quartic (1) by making a substitution
of the form
![]() to (10) gives
to (10) gives
![]() be a Real Root of the resolvent Cubic Equation
be a Real Root of the resolvent Cubic Equation