The differential equation describing exponential growth is
 |
(1) |
This can be integrated directly
 |
(2) |
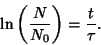 |
(3) |
Exponentiating,
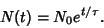 |
(4) |
Defining
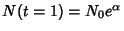 gives
gives 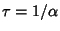 in (4), so
in (4), so
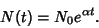 |
(5) |
The quantity 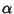 in this equation is sometimes known as the Malthusian Parameter.
in this equation is sometimes known as the Malthusian Parameter.
Consider a more complicated growth law
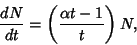 |
(6) |
where 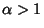 is a constant. This can also be integrated directly
is a constant. This can also be integrated directly
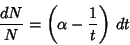 |
(7) |
 |
(8) |
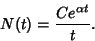 |
(9) |
Note that this expression blows up at 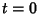 . We are given the Initial Condition
that
. We are given the Initial Condition
that
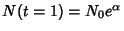 , so
, so  .
.
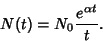 |
(10) |
The 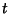 in the Denominator of (10) greatly suppresses the growth in the long run
compared to the simple growth law.
in the Denominator of (10) greatly suppresses the growth in the long run
compared to the simple growth law.
The Logistic Growth Curve, defined by
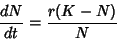 |
(11) |
is another growth law which frequently arises in biology. It has a rather complicated solution for 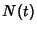 .
.
See also Gompertz Curve, Life Expectancy, Logistic Growth Curve, Lotka-Volterra Equations,
Makeham Curve, Malthusian Parameter, Survivorship Curve
© 1996-9 Eric W. Weisstein
1999-05-26