|
|
|
A primality certificate based on Fermat's Little Theorem Converse. Although the general idea had been well-established for some time, Pratt became the first to prove that the certificate tree was of polynomial size and could also be verified in polynomial time. He was also the first to observe that the tree implies that Primes are in the complexity class NP.
To generate a Pratt certificate, assume that ![]() is a Positive Integer and
is a Positive Integer and ![]() is the set of Prime
Factors of
is the set of Prime
Factors of ![]() . Suppose there exists an Integer
. Suppose there exists an Integer ![]() (called a ``Witness'') such that
(called a ``Witness'') such that
![]() but
but
![]() (mod
(mod ![]() ) whenever
) whenever ![]() is one of
is one of ![]() . Then Fermat's Little Theorem
Converse states that
. Then Fermat's Little Theorem
Converse states that ![]() is Prime (Wagon 1991, pp. 278-279).
is Prime (Wagon 1991, pp. 278-279).
By applying Fermat's Little Theorem Converse to ![]() and recursively to each purported factor of
and recursively to each purported factor of ![]() , a certificate for a given Prime Number can be generated. Stated
another way, the Pratt certificate gives a proof that a number
, a certificate for a given Prime Number can be generated. Stated
another way, the Pratt certificate gives a proof that a number ![]() is a Primitive Root of the multiplicative
Group (mod
is a Primitive Root of the multiplicative
Group (mod ![]() ) which, along with the fact that
) which, along with the fact that ![]() has order
has order ![]() , proves that
, proves that ![]() is a Prime.
is a Prime.
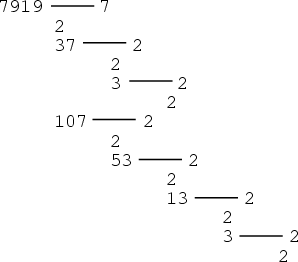
The figure above gives a certificate for the primality of ![]() . The numbers to the right of the dashes are
Witnesses to the numbers to left. The set
. The numbers to the right of the dashes are
Witnesses to the numbers to left. The set ![]() for
for ![]() is given by
is given by
![]() . Since
. Since
![]() but
but ![]() ,
, ![]() ,
,
![]() (mod 7919), 7 is a Witness for
7919. The Prime divisors of
(mod 7919), 7 is a Witness for
7919. The Prime divisors of ![]() are 2, 37, and 107. 2 is a so-called ``self-Witness'' (i.e., it is
recognized as a Prime without further ado), and the remainder of the witnesses are shown as a nested tree. Together, they
certify that 7919 is indeed Prime. Because it requires the Factorization of
are 2, 37, and 107. 2 is a so-called ``self-Witness'' (i.e., it is
recognized as a Prime without further ado), and the remainder of the witnesses are shown as a nested tree. Together, they
certify that 7919 is indeed Prime. Because it requires the Factorization of ![]() , the Method of Pratt
certificates is best applied to small numbers (or those numbers
, the Method of Pratt
certificates is best applied to small numbers (or those numbers ![]() known to have easily factorable
known to have easily factorable ![]() ).
).
A Pratt certificate is quicker to generate for small numbers than are other types of primality certificates. The Mathematica
![]() (Wolfram Research, Champaign, IL) task ProvablePrime[n] therefore generates an
Atkin-Goldwasser-Kilian-Morain Certificate only for numbers above a certain limit (
(Wolfram Research, Champaign, IL) task ProvablePrime[n] therefore generates an
Atkin-Goldwasser-Kilian-Morain Certificate only for numbers above a certain limit (![]() by default), and a Pratt
certificate for smaller numbers.
by default), and a Pratt
certificate for smaller numbers.
See also Atkin-Goldwasser-Kilian-Morain Certificate, Fermat's Little Theorem Converse, Primality Certificate, Witness
References
Pratt, V. ``Every Prime Has a Succinct Certificate.'' SIAM J. Comput. 4, 214-220, 1975.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 278-285, 1991.
Wilf, H. §4.10 in Algorithms and Complexity. Englewood Cliffs, NJ: Prentice-Hall, 1986.
|
|
|
© 1996-9 Eric W. Weisstein