|
|
|
Probability is the branch of mathematics which studies the possible outcomes of given events together with their relative likelihoods and distributions. In common usage, the word ``probability'' is used to mean the chance that a particular event (or set of events) will occur expressed on a linear scale from 0 (impossibility) to 1 (certainty), also expressed as a Percentage between 0 and 100%. The analysis of events governed by probability is called Statistics.
There are several competing interpretations of the actual ``meaning'' of probabilities. Frequentists view probability simply as a measure of the frequency of outcomes (the more conventional interpretation), while Bayesians treat probability more subjectively as a statistical procedure which endeavors to estimate parameters of an underlying distribution based on the observed distribution.
A properly normalized function which assigns a probability ``density'' to each possible outcome within some interval is called a Probability Function, and its cumulative value (integral for a continuous distribution or sum for a discrete distribution) is called a Distribution Function.
Probabilities are defined to obey certain assumptions, called the Probability Axioms. Let a Sample Space contain
the Union (![]() ) of all possible events
) of all possible events ![]() , so
, so
 |
(1) |
| (2) |
| (3) |
| (4) |
Let ![]() denote the Conditional Probability of
denote the Conditional Probability of ![]() given that
given that ![]() has already occurred, then
has already occurred, then
| (5) | |||
| (6) | |||
| (7) | |||
| (8) | |||
| (9) | |||
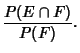 |
(10) |
| (11) |
|
|
|
|
|
|
|
|
(12) |
See also Bayes' Formula, Conditional Probability, Distribution, Distribution Function, Likelihood, Probability Axioms, Probability Function, Probability Inequality, Statistics
|
|
|
© 1996-9 Eric W. Weisstein