|
|
|
The distribution function ![]() , sometimes also called the Probability Distribution Function, describes the
probability that a trial
, sometimes also called the Probability Distribution Function, describes the
probability that a trial ![]() takes on a value less than or equal to a number
takes on a value less than or equal to a number ![]() . The distribution function is therefore
related to a continuous Probability Density Function
. The distribution function is therefore
related to a continuous Probability Density Function ![]() by
by
| (1) |
| (2) |
| (3) |
A Joint Distribution Function can be defined if outcomes are dependent on two parameters:
| (4) | |||
| (5) | |||
| (6) |
| (7) |
Given a continuous ![]() , assume you wish to generate numbers distributed as
, assume you wish to generate numbers distributed as ![]() using a random number generator.
If the random number generator yields a uniformly distributed value
using a random number generator.
If the random number generator yields a uniformly distributed value ![]() in [0,1] for each trial
in [0,1] for each trial ![]() , then compute
, then compute
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
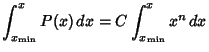 |
|||
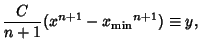 |
(14) |
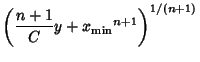 |
|||
| (15) |
A distribution with constant Variance of ![]() for all values of
for all values of ![]() is known as a Homoscedastic distribution.
The method of finding the value at which the distribution is a maximum is known as the Maximum Likelihood method.
is known as a Homoscedastic distribution.
The method of finding the value at which the distribution is a maximum is known as the Maximum Likelihood method.
See also Bernoulli Distribution, Beta Distribution, Binomial Distribution, Bivariate Distribution, Cauchy Distribution, Chi Distribution, Chi-Squared Distribution, Cornish-Fisher Asymptotic Expansion, Correlation Coefficient, Distribution, Double Exponential Distribution, Equally Likely Outcomes Distribution, Exponential Distribution, Extreme Value Distribution, F-Distribution, Fermi-Dirac Distribution, Fisher's z-Distribution, Fisher-Tippett Distribution, Gamma Distribution, Gaussian Distribution, Geometric Distribution, Half-Normal Distribution, Hypergeometric Distribution, Joint Distribution Function, Laplace Distribution, Lattice Distribution, Lévy Distribution, Logarithmic Distribution, Log-Series Distribution, Logistic Distribution, Lorentzian Distribution, Maxwell Distribution, Negative Binomial Distribution, Normal Distribution, Pareto Distribution, Pascal Distribution, Pearson Type III Distribution, Poisson Distribution, Pólya Distribution, Ratio Distribution, Rayleigh Distribution, Rice Distribution, Snedecor's F-Distribution, Student's t-Distribution, Student's z-Distribution, Uniform Distribution, Weibull Distribution
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Probability Functions.'' Ch. 26 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 925-964, 1972.
Iyanaga, S. and Kawada, Y. (Eds.). ``Distribution of Typical Random Variables.'' Appendix A, Table 22 in
Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1483-1486,
1980.
|
|
|
© 1996-9 Eric W. Weisstein