Rose

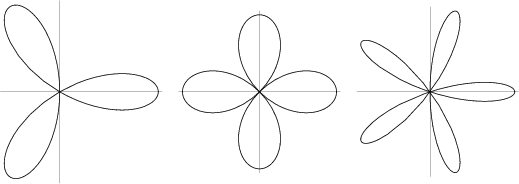
A curve which has the shape of a petalled flower. This curve was named Rhodonea by the Italian mathematician Guido Grandi between 1723 and 1728 because it resembles a rose (MacTutor Archive). The polar equation of the rose is

$$r=a\sin(n\theta),$$

or

$$r=a\cos(n\theta).$$

If $n$ is Odd, the rose is $n$-petalled. If $n$ is Even, the rose is $2n$-petalled. If $n$ is Irrational, then there are an infinite number of petals.

The Quadrifolium is the rose with $n=2$. The rose is the Radial Curve of the Epicycloid.

See also Daisy, Maurer Rose, Starr Rose

References

Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 175-177, 1972.

Lee, X. ``Rose.'' http://www.best.com/~xah/SpecialPlaneCurves_dir/Rose_dir/rose.html.

MacTutor History of Mathematics Archive. ``Rhodonea Curves.'' http://www-groups.dcs.st-and.ac.uk/~history/Curves/Rhodonea.html.

Wagon, S. ``Roses.'' §4.1 in Mathematica in Action. New York: W. H. Freeman, pp. 96-102, 1991.