If the sides of a Triangle are divided in the ratios 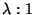 ,
, 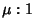 , and
, and 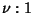 , the Cevians form a central Triangle whose Area is
, the Cevians form a central Triangle whose Area is
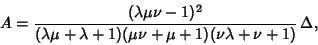 |
(1) |
where  is the Area of the original Triangle. For
is the Area of the original Triangle. For
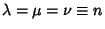 ,
,
 |
(2) |
For 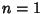 , 2, 3, ..., the areas are 0, 1/7, 4/13, 3/7, 16/31, 25/43, .... The Area of the Triangle formed by
connecting the division points on each side is
, 2, 3, ..., the areas are 0, 1/7, 4/13, 3/7, 16/31, 25/43, .... The Area of the Triangle formed by
connecting the division points on each side is
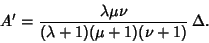 |
(3) |
Routh's theorem gives Ceva's Theorem and Menelaus' Theorem as special cases.
See also Ceva's Theorem, Cevian, Menelaus' Theorem
References
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, pp. 211-212, 1969.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() ,
, ![]() , and
, and ![]() , the Cevians form a central Triangle whose Area is
, the Cevians form a central Triangle whose Area is