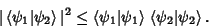 |
(1) |
Written out explicitly
![\begin{displaymath}
\left[{\int_a^b \psi_1(x)\psi_2(x)\,dx}\right]^2\leq \int_a^b [\psi_1(x)]^2\,dx \int_a^b [\psi_2(x)]^2\,dx,
\end{displaymath}](s1_361.gif) |
(2) |
with equality Iff
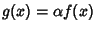 with
with 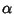 a constant. To derive, let
a constant. To derive, let 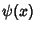 be a
Complex function and
be a
Complex function and 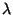 a Complex constant such that
a Complex constant such that
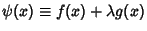 for some
for some 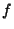 and
and 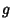 . Since
. Since
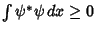 ,
,
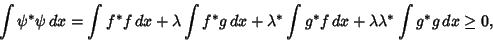 |
(3) |
with equality when 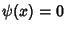 . Set
. Set
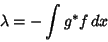 |
(4) |
so that
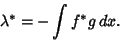 |
(5) |
Plugging (5) and (4) into (3) then gives
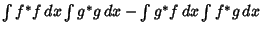
|
|
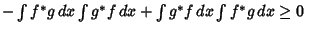
|
(6) |
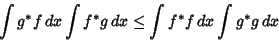 |
(7) |
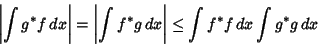 |
(8) |
so
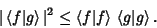 |
(9) |
Bessel's Inequality can be derived from this.
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 11, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 527-529, 1985.
© 1996-9 Eric W. Weisstein
1999-05-26
![\begin{displaymath}
\left[{\int_a^b \psi_1(x)\psi_2(x)\,dx}\right]^2\leq \int_a^b [\psi_1(x)]^2\,dx \int_a^b [\psi_2(x)]^2\,dx,
\end{displaymath}](s1_361.gif)