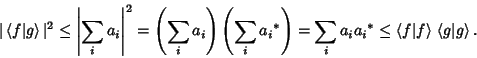If 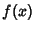 is piecewise Continuous and has a general Fourier Series
is piecewise Continuous and has a general Fourier Series
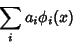 |
(1) |
with Weighting Function 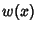 , it must be true that
, it must be true that
![\begin{displaymath}
\int \left[{f(x)-\sum_i a_i\phi_i(x)}\right]^2 w(x)\, dx \geq 0
\end{displaymath}](b_938.gif) |
(2) |
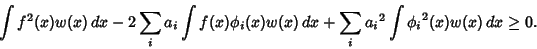 |
(3) |
But the Coefficient of the generalized Fourier Series is given by
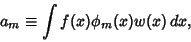 |
(4) |
so
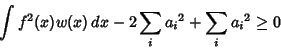 |
(5) |
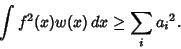 |
(6) |
Equation (6) is an inequality if the functions 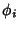 are not Complete. If they are
Complete, then the inequality (2) becomes an equality, so (6) becomes an
equality and is known as Parseval's Theorem. If
are not Complete. If they are
Complete, then the inequality (2) becomes an equality, so (6) becomes an
equality and is known as Parseval's Theorem. If 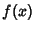 has a simple Fourier Series expansion with
Coefficients
has a simple Fourier Series expansion with
Coefficients 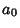 ,
, 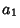 ,
, 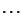 ,
, 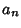 and
and 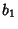 , ...,
, ..., 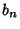 , then
, then
![\begin{displaymath}
{\textstyle{1\over 2}}{a_0}^2 + \sum\limits_{k=1}^\infty ({a_k}^2+{b_k}^2) \leq {1\over\pi}\int^\pi_{-\pi} [f(x)]^2\,dx.
\end{displaymath}](b_948.gif) |
(7) |
The inequality can also be derived from Schwarz's Inequality
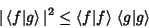 |
(8) |
by expanding 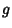 in a superposition of Eigenfunctions of
in a superposition of Eigenfunctions of 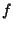 ,
,
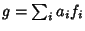 . Then
. Then
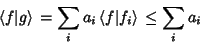 |
(9) |
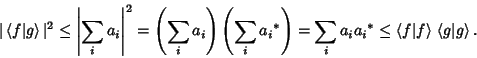 |
(10) |
If 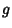 is normalized, then
is normalized, then
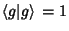 and
and
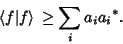 |
(11) |
See also Schwarz's Inequality, Triangle Inequality
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 526-527, 1985.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, p. 1102, 1980.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is piecewise Continuous and has a general Fourier Series
is piecewise Continuous and has a general Fourier Series
![\begin{displaymath}
\int \left[{f(x)-\sum_i a_i\phi_i(x)}\right]^2 w(x)\, dx \geq 0
\end{displaymath}](b_938.gif)
![\begin{displaymath}
{\textstyle{1\over 2}}{a_0}^2 + \sum\limits_{k=1}^\infty ({a_k}^2+{b_k}^2) \leq {1\over\pi}\int^\pi_{-\pi} [f(x)]^2\,dx.
\end{displaymath}](b_948.gif)