A solenoidal Vector Field satisfies
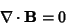 |
(1) |
for every Vector 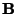 , where
, where
 is the Divergence.
If this condition is satisfied, there exists a vector
is the Divergence.
If this condition is satisfied, there exists a vector 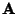 , known as the
Vector Potential, such that
, known as the
Vector Potential, such that
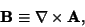 |
(2) |
where
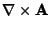 is the Curl. This follows from the vector identity
is the Curl. This follows from the vector identity
 |
(3) |
If 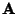 is an Irrotational Field, then
is an Irrotational Field, then
 |
(4) |
is solenoidal. If 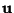 and
and 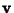 are irrotational, then
are irrotational, then
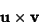 |
(5) |
is solenoidal. The quantity
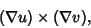 |
(6) |
where  is the Gradient, is always solenoidal. For a function
is the Gradient, is always solenoidal. For a function 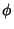 satisfying Laplace's Equation
satisfying Laplace's Equation
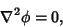 |
(7) |
it follows that  is solenoidal (and also Irrotational).
is solenoidal (and also Irrotational).
See also Beltrami Field, Curl, Divergence, Divergenceless Field, Gradient, Irrotational Field,
Laplace's Equation, Vector Field
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, pp. 1084, 1980.
© 1996-9 Eric W. Weisstein
1999-05-26