|
|
|
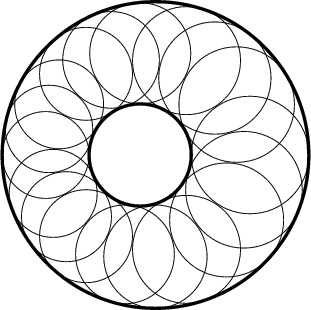
If a Steiner Chain is formed from one starting circle, then a Steiner Chain is formed from any other starting circle. In other words, given two nonconcentric Circles, draw Circles successively touching them and each other. If the last touches the first, this will also happen for any position of the first Circle.
See also Hexlet, Steiner Chain
References
Coxeter, H. S. M. ``Interlocking Rings of Spheres.'' Scripta Math. 18, 113-121, 1952.
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, p. 87, 1969.
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 124-126,
1967.
Forder, H. G. Geometry, 2nd ed. London: Hutchinson's University Library, p. 23, 1960.
Gardner, M. ``Mathematical Games: The Diverse Pleasures of Circles that Are Tangent to One Another.'' Sci. Amer. 240,
18-28, Jan. 1979.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle.
Boston, MA: Houghton Mifflin, pp. 113-115, 1929.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 53-54, 1990.