|
|
|
Abramowitz and Stegun (1972, pp. 496-499) define the Struve function as
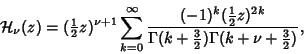 |
(1) |
| (2) |
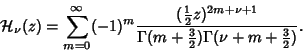 |
(3) |
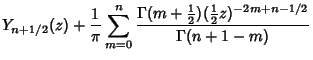 |
(4) | ||
| (5) |
| (6) |
See also Anger Function, Bessel Function, Modified Struve Function, Weber Functions
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Struve Function
Spanier, J. and Oldham, K. B. ``The Struve Function.'' Ch. 57 in An Atlas of Functions.
Washington, DC: Hemisphere, pp. 563-571, 1987.
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University
Press, 1966.
![]() .'' §12.1 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 496-498, 1972.
.'' §12.1 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 496-498, 1972.