Tangle

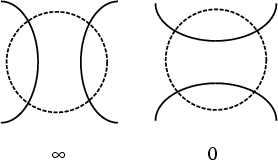
A region in a Knot or Link projection plane surrounded by a Circle such that the Knot or Link crosses the circle exactly four times. Two tangles are equivalent if a sequence of Reidemeister Moves can be used to transform one into the other while keeping the four string endpoints fixed and not allowing strings to pass outside the Circle.

The simplest tangles are the $\infty$-tangle and 0-tangle, shown above. A tangle with $n$ left-handed twists is called an $n$-tangle, and one with $n$ right-handed twists is called a $-n$-tangle. By placing tangles side by side, more complicated tangles can be built up such as ($-2$, 3, 2), etc. The link created by connecting the ends of the tangles is now described by the sequence of tangle symbols, known as Conway's Knot Notation. If tangles are multiplied by 0 and then added, the resulting tangle symbols are separated by commas. Additional symbols which are used are the period, colon, and asterisk.

Amazingly enough, two tangles described in this Notation are equivalent Iff the Continued Fractions of the form

$$2+{\strut\displaystyle 1\over\strut\displaystyle 3+{\strut\displaystyle 1\over\strut\displaystyle -2}}$$

are equal (Burde and Zieschang 1985)! An Algebraic Tangle is any tangle obtained by Additions and Multiplications of rational tangles (Adams 1994). Not all tangles are Algebraic.

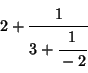
See also Algebraic Link, Flype, Pretzel Knot

References

Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman pp. 41-51, 1994.

Burde, G. and Zieschang, H. Knots. Berlin: de Gruyter, 1985.