|
|
|
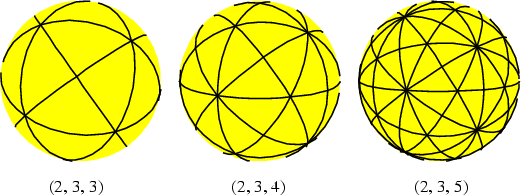
Given a Triangle with angles (![]() ,
, ![]() ,
, ![]() ), the resulting symmetry Group is called a
), the resulting symmetry Group is called a ![]() triangle group (also known as a Spherical Tessellation). In 3-D, such Groups must satisfy
triangle group (also known as a Spherical Tessellation). In 3-D, such Groups must satisfy
See also Geodesic Dome
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 155-161, 1987.
Coxeter, H. S. M. ``The Partition of a Sphere According to the Icosahedral Group.'' Scripta Math 4, 156-157, 1936.
Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, 1973.
Kraitchik, M. ``A Mosaic on the Sphere.'' §7.3 in Mathematical Recreations. New York: W. W. Norton, pp. 208-209, 1942.