Tessellation

A regular Tiling of Polygons (in 2-D), Polyhedra (3-D), or Polytopes ($n$-D) is called a tessellation. Tessellations can be specified using a Schläfli Symbol.

Consider a 2-D tessellation with $q$ regular $p$-gons at each Vertex. In the Plane,

$$\left({1-{2\over p}}\right)\pi = {2\pi\over q}$$ (1)

$${1\over p}+{1\over q}={1\over 2},$$ (2)

so

$$(p-2)(q-2)=4$$ (3)

(Ball and Coxeter 1987), and the only factorizations are

$$4 = 4\cdot 1=(6-2)(3-2) \Rightarrow \{6,3\}$$ (4)

$$= 2\cdot 2=(4-2)(4-2) \Rightarrow \{4,4\}$$ (5)

$$= 1\cdot 4=(3-2)(6-2) \Rightarrow \{3,6\}.$$ (6)

Therefore, there are only three regular tessellations (composed of the Hexagon, Square, and Triangle), illustrated as follows.

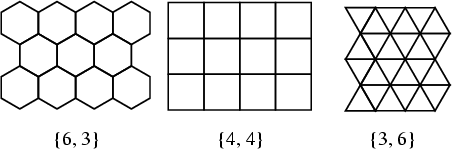
There do not exist any regular Star Polygon tessellations in the Plane. Regular tessellations of the Sphere by Spherical Triangles are called Triangular Symmetry Groups.

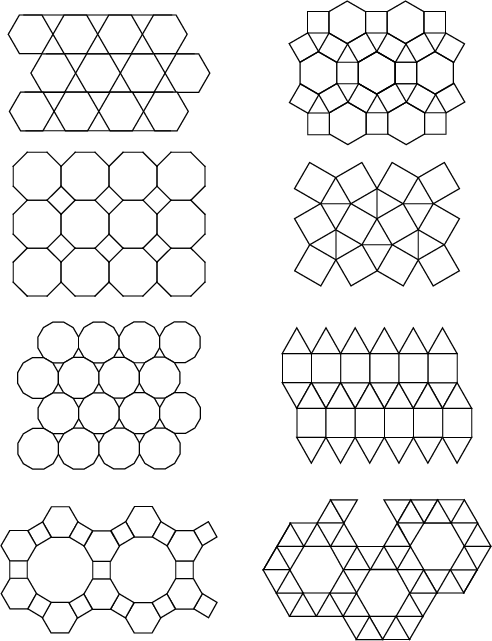
Regular tilings of the plane by two or more convex regular Polygons such that the same Polygons in the same order surround each Vertex are called semiregular tilings. In the plane, there are eight such tessellations, illustrated below.

In 3-D, a Polyhedron which is capable of tessellating space is called a Space-Filling Polyhedron. Examples include the Cube, Rhombic Dodecahedron, and Truncated Octahedron. There is also a 16-sided space-filler and a convex Polyhedron known as the Schmitt-Conway Biprism which fills space only aperiodically.

A tessellation of $n$-D polytopes is called a Honeycomb.

See also Archimedean Solid, Cell, Honeycomb, Schläfli Symbol, Semiregular Polyhedron, Space-Filling Polyhedron, Tiling, Triangular Symmetry Group

References

Tilings

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 105-107, 1987.

Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 60-63, 1989.

Gardner, M. Martin Gardner's New Mathematical Diversions from Scientific American. New York: Simon and Schuster, pp. 201-203, 1966.

Gardner, M. ``Tilings with Convex Polygons.'' Ch. 13 in Time Travel and Other Mathematical Bewilderments. New York: W. H. Freeman, pp. 162-176, 1988.

Kraitchik, M. ``Mosaics.'' §8.2 in Mathematical Recreations. New York: W. W. Norton, pp. 199-207, 1942.

Lines, L. Solid Geometry. New York: Dover, pp. 199 and 204-207 1965.

Pappas, T. ``Tessellations.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 120-122, 1989.

Peterson, I. The Mathematical Tourist: Snapshots of Modern Mathematics. New York: W. H. Freeman, p. 75, 1988.

Rawles, B. Sacred Geometry Design Sourcebook: Universal Dimensional Patterns. Nevada City, CA: Elysian Pub., 1997.

Walsh, T. R. S. ``Characterizing the Vertex Neighbourhoods of Semi-Regular Polyhedra.'' Geometriae Dedicata 1, 117-123, 1972.