Tesseract

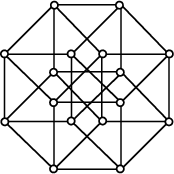
The Hypercube in $\Bbb{R}^4$ is called a tesseract. It has the Schläfli Symbol $\{4, 3, 3\}$, and Vertices $(\pm 1, \pm 1, \pm 1, \pm 1)$. The above figures show two visualizations of the tesseract. The figure on the left is a projection of the tesseract in 3-space (Gardner 1977), and the figure on the right is the Graph of the tesseract symmetrically projected into the Plane (Coxeter 1973). A tesseract has 16 Vertices, 32 Edges, 24 Squares, and 8 Cubes.

See also Hypercube, Polytope

References

Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, p. 123, 1973.

Gardner, M. ``Hypercubes.'' Ch. 4 in Mathematical Carnival: A New Round-Up of Tantalizers and Puzzles from Scientific American. New York: Vintage Books, 1977.

Geometry Center. ``The Tesseract (or Hypercube).'' http://www.geom.umn.edu/docs/outreach/4-cube/.