Hypercube

The generalization of a 3-Cube to $n$-D, also called a Measure Polytope. It is a regular Polytope with mutually Perpendicular sides, and is therefore an Orthotope. It is denoted $\gamma_n$ and has Schläfli Symbol 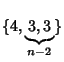. The number of $k$-cubes contained in an $n$-cube can be found from the Coefficients of $(2k+1)^n$.

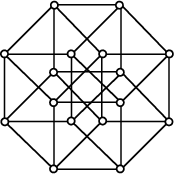
The 1-hypercube is a Line Segment, the 2-hypercube is the Square, and the 3-hypercube is the Cube. The hypercube in $\Bbb{R}^4$, called a Tesseract, has the Schläfli Symbol $\{4, 3, 3\}$ and Vertices $(\pm 1, \pm 1, \pm 1, \pm 1)$. The above figures show two visualizations of the Tesseract. The figure on the left is a projection of the Tesseract in 3-space (Gardner 1977), and the figure on the right is the Graph of the Tesseract symmetrically projected into the Plane (Coxeter 1973). A Tesseract has 16 Vertices, 32 Edges, 24 Squares, and eight Cubes.

See also Cross Polytope, Cube, Hypersphere, Orthotope, Parallelepiped, Polytope, Simplex, Tesseract

References

Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, p. 123, 1973.

Gardner, M. ``Hypercubes.'' Ch. 4 in Mathematical Carnival: A New Round-Up of Tantalizers and Puzzles from Scientific American. New York: Vintage Books, 1977.

Geometry Center. ``The Tesseract (or Hypercube).'' http://www.geom.umn.edu/docs/outreach/4-cube/.

Pappas, T. ``How Many Dimensions are There?'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 204-205, 1989.