|
|
|
|
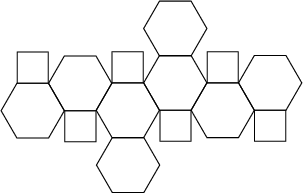
An Archimedean Solid, also known as the Mecon, whose Dual Polyhedron is the Tetrakis
Hexahedron. It is also Uniform Polyhedron ![]() and has Schläfli Symbol t
and has Schläfli Symbol t![]() and Wythoff Symbol
and Wythoff Symbol ![]() .
The faces of the truncated octahedron are
.
The faces of the truncated octahedron are ![]() . The truncated octahedron has the
. The truncated octahedron has the ![]() Octahedral Group of symmetries.
Octahedral Group of symmetries.
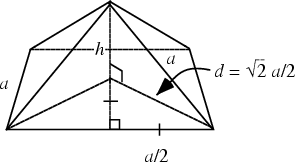
The solid can be formed from an Octahedron via Truncation by removing six Square Pyramids, each with edge slant height ![]() and height
and height ![]() , where
, where ![]() is the side length of the original
Octahedron. From the above diagram, the height and base area of the Square Pyramid are
is the side length of the original
Octahedron. From the above diagram, the height and base area of the Square Pyramid are
| (1) | |||
| (2) |
| (3) |
| (4) |
The truncated octahedron is a Space-Filling Polyhedron. The Inradius, Midradius, and
Circumradius for ![]() are
are
| (5) | |||
| (6) | |||
| (7) |
See also Octahedron, Square Pyramid, Truncation
References
Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, pp. 29-30 and 257, 1973.
|
|
|
© 1996-9 Eric W. Weisstein