|
|
|
A plane-filling arrangement of plane figures or its generalization to higher dimensions. Formally, a tiling is a collection of disjoint open sets, the closures of which cover the plane. Given a single tile, the so-called first Corona is the set of all tiles that have a common boundary point with the tile (including the original tile itself).
Wang's Conjecture (1961) stated that if a set of tiles tiled the plane, then they could always be arranged to do so periodically. A periodic tiling of the Plane by Polygons or Space by Polyhedra is called a Tessellation. The conjecture was refuted in 1966 when R. Berger showed that an aperiodic set of 20,426 tiles exists. By 1971, R. Robinson had reduced the number to six and, in 1974, R. Penrose discovered an aperiodic set (when color-matching rules are included) of two tiles: the so-called Penrose Tiles. (Penrose also sued the Kimberly Clark Corporation over their quilted toilet paper, which allegedly resembles a Penrose aperiodic tiling; Mirsky 1997.)
It is not known if there is a single aperiodic tile.
| tilings | |
| 3 | any |
| 4 | any |
| 5 | 14 |
| 6 | 3 |
The number of tilings possible for convex irregular Polygons are given in the above table. Any
Triangle or convex Quadrilateral tiles the plane. There are at least 14 classes of convex
Pentagonal tilings. There are at least three aperiodic tilings of Hexagons, given
by the following types:
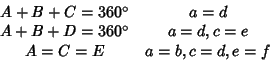 |
(1) |
| (2) |
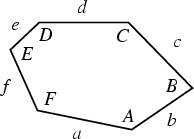
There are no tilings for convex ![]() -gons for
-gons for ![]() .
.
See also Anisohedral Tiling, Corona (Tiling), Gosper Island, Heesch's Problem, Isohedral Tiling, Koch Snowflake, Monohedral Tiling, Penrose Tiles, Polyomino Tiling, Space-Filling Polyhedron, Tiling Theorem, Triangle Tiling
References
Eppstein, D. ``Tiling.''
http://www.ics.uci.edu/~eppstein/junkyard/tiling.html.
Gardner, M. ``Tilings with Convex Polygons.'' Ch. 13 in Time Travel and Other Mathematical Bewilderments.
New York: W. H. Freeman, pp. 162-176, 1988.
Gardner, M. Chs. 1-2 in Penrose Tiles to Trapdoor Ciphers... and the Return of Dr. Matrix, reissue ed.
Washington, DC: Math. Assoc. Amer.
Grünbaum, B. and Shepard, G. C. ``Some Problems on Plane Tilings.'' In The Mathematical Gardner
(Ed. D. Klarner). Boston, MA: Prindle, Weber, and Schmidt, pp. 167-196, 1981.
Grünbaum, B. and Sheppard, G. C. Tilings and Patterns. New York: W. H. Freeman, 1986.
Lee, X. ``Visual Symmetry.''
http://www.best.com/~xah/MathGraphicsGallery_dir/Tiling_dir/tiling.html.
Mirsky, S. ``The Emperor's New Toilet Paper.'' Sci. Amer. 277, 24, July 1997.
Pappas, T. ``Mathematics & Moslem Art.'' The Joy of Mathematics.
San Carlos, CA: Wide World Publ./Tetra, p. 178, 1989.
Peterson, I. The Mathematical Tourist: Snapshots of Modern Mathematics. New York: W. H. Freeman, pp. 82-85, 1988.
Rawles, B. Sacred Geometry Design Sourcebook: Universal Dimensional Patterns. Nevada City, CA: Elysian Pub., 1997.
Schattschneider, D. ``In Praise of Amateurs.'' In The Mathematical Gardner (Ed. D. Klarner). Boston, MA:
Prindle, Weber, and Schmidt, pp. 140-166, 1981.
Seyd, J. A. and Salman, A. S. Symmetries of Islamic Geometrical Patterns. River Edge, NJ: World Scientific, 1995.
Stein, S. and Szabó, S. Algebra and Tiling. Washington, DC: Math. Assoc. Amer., 1994.
![]() Tilings
Tilings
|
|
|
© 1996-9 Eric W. Weisstein