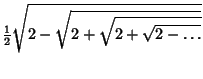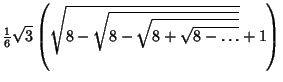The exact values of 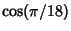 and
and 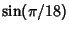 are given by infinite Nested Radicals.
are given by infinite Nested Radicals.
where the sequence of signs +, +,  repeats with period 3, and
repeats with period 3, and
where the sequence of signs  ,
,  , + repeats with period 3.
, + repeats with period 3.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() and
and ![]() are given by infinite Nested Radicals.
are given by infinite Nested Radicals.