|
|
|
Let ![]() be an Irregular Prime, and let
be an Irregular Prime, and let ![]() be a Prime with
be a Prime with ![]() . Also let
. Also let ![]() be an Integer such
that
be an Integer such
that
![]() (mod
(mod ![]() ). For an Irregular Pair
). For an Irregular Pair ![]() , form the product
, form the product
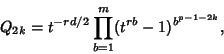
 |
See also Fermat's Last Theorem, Irregular Pair, Irregular Prime
References
Johnson, W. ``Irregular Primes and Cyclotomic Invariants.'' Math. Comput. 29, 113-120, 1975.