Solution of a system of second-order homogeneous ordinary differential equations with constant Coefficients of the form
where B is a Positive Definite Matrix. To solve the vibration problem,
- 1. Solve the Characteristic Equation of B to get Eigenvalues
 , ...,
, ...,
 . Define
. Define
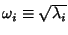 .
.
- 2. Compute the corresponding Eigenvectors
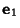 , ...,
, ..., 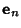 .
.
- 3. The normal modes of oscillation are given by
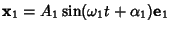 , ...,
, ...,
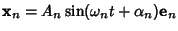 , where
, where 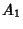 , ...,
, ..., 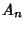 and
and 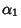 , ...,
, ..., 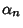 are arbitrary
constants.
are arbitrary
constants.
- 4. The general solution is
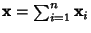 .
.
© 1996-9 Eric W. Weisstein
1999-05-26