|
|
|
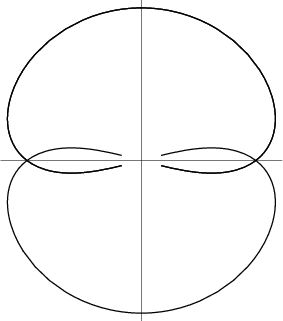
A curve named after James Watt (1736-1819), the Scottish engineer who developed the steam engine (MacTutor Archive).
The curve is produced by a Linkage of rods connecting two wheels of equal diameter. Let the two wheels
have Radius ![]() and let their centers be located a distance
and let their centers be located a distance ![]() apart. Further suppose that a rod of length
apart. Further suppose that a rod of length ![]() is fixed at each end to the Circumference of the two wheels. Let
is fixed at each end to the Circumference of the two wheels. Let ![]() be the Midpoint of the rod. Then Watt's
curve
be the Midpoint of the rod. Then Watt's
curve ![]() is the Locus of
is the Locus of ![]() .
.
The Polar equation of Watt's curve is
References
Lockwood, E. H. A Book of Curves. Cambridge, England: Cambridge University Press, p. 162, 1967.
MacTutor History of Mathematics Archive. ``Watt's Curve.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Watts.html.