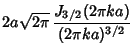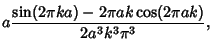The Apodization Function
Its Full Width at Half Maximum is 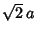 . Its Instrument Function is
. Its Instrument Function is
where 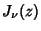 is a Bessel Function of the First Kind. It has a width of 1.59044, a maximum of
is a Bessel Function of the First Kind. It has a width of 1.59044, a maximum of
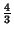 ,
maximum Negative sidelobe of
,
maximum Negative sidelobe of 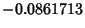 times the peak, and maximum Positive sidelobe of 0.356044 times the peak.
times the peak, and maximum Positive sidelobe of 0.356044 times the peak.
See also Apodization Function, Instrument Function
References
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed.
Cambridge, England: Cambridge University Press, p. 547, 1992.
© 1996-9 Eric W. Weisstein
1999-05-26