|
|
|
The Wigner ![]() symbols are written
symbols are written
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
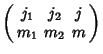 |
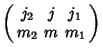 |
||
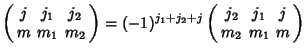 |
|||
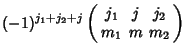 |
|||
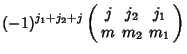 |
|||
 |
(7) |
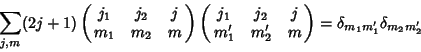 |
(8) |
 |
(9) |
General formulas are very complicated, but some specific cases are

|
|
![$ \times\left[{{(2j_1)!(2j_2)!\over (2j_1+2j_2+1)!(j_1+m_1)!}{(j_1+j_2+m_1+m_2)!(j_1+j_2-m_1-m_2)!\over (j_1-m_1)!(j_2+m_2)!(j_2-m_2)!}}\right]^{1/2}\quad$](w_920.gif)
|
(10) |
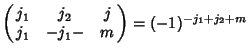
|
|
![$\times\left[{{(2j_1)!(-j_1+j_2+j)!\over (j_1+j_2+j+1)!(j_1-j_2+j)!}{(j_1+j_2+m)!(j-m)!\over (j_1+j_2-j)!(-j_1+j_2-m)!(j+m)!}}\right]^{1/2}\quad$](w_922.gif)
|
(11) |
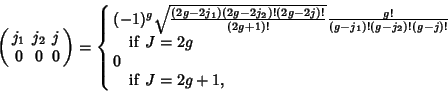 |
(12) |
For Spherical Harmonics
![]() ,
,
|
|
|
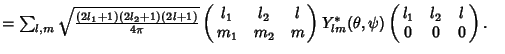
|
(13) |
|
|
|

|
(14) |
| (15) |
See also Clebsch-Gordan Coefficient, Racah V-Coefficient, Racah W-Coefficient, Wigner 6j-Symbol, Wigner 9j-Symbol
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Vector-Addition Coefficients.'' §27.9 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 1006-1010, 1972.
Condon, E. U. and Shortley, G. The Theory of Atomic Spectra. Cambridge, England: Cambridge University Press, 1951.
de Shalit, A. and Talmi, I. Nuclear Shell Theory. New York: Academic Press, 1963.
Gordy, W. and Cook, R. L. Microwave Molecular Spectra, 3rd ed. New York: Wiley, pp. 804-811, 1984.
Messiah, A. ``Clebsch-Gordan (C.-G.) Coefficients and `
Rotenberg, M.; Bivens, R.; Metropolis, N.; and Wooten, J. K. The
Shore, B. W. and Menzel, D. H. Principles of Atomic Spectra. New York: Wiley, pp. 275-276, 1968.
Sobel'man, I. I. ``Angular Momenta.'' Ch. 4 in Atomic Spectra and Radiative Transitions, 2nd ed.
Berlin: Springer-Verlag, 1992.
Wigner, E. P. Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra, expanded and improved ed.
New York: Academic Press, 1959.
![]() ' Symbols.'' Appendix C.I in Quantum Mechanics, Vol. 2.
Amsterdam, Netherlands: North-Holland, pp. 1054-1060, 1962.
' Symbols.'' Appendix C.I in Quantum Mechanics, Vol. 2.
Amsterdam, Netherlands: North-Holland, pp. 1054-1060, 1962.
![]() and
and ![]() Symbols. Cambridge, MA: MIT Press, 1959.
Symbols. Cambridge, MA: MIT Press, 1959.
|
|
|
© 1996-9 Eric W. Weisstein