|
|
|
A generalization of Clebsch-Gordan Coefficients and Wigner
3j-Symbol and Wigner 6j-Symbol which arises in the coupling of four angular momenta and can
be written in terms of the Wigner 3j-Symbol and Wigner 6j-Symbol.
Let tensor operators ![]() and
and ![]() act, respectively, on subsystems 1 and 2. Then the reduced matrix element
of the product
act, respectively, on subsystems 1 and 2. Then the reduced matrix element
of the product
![]() of these two irreducible operators in the coupled representation is given
in terms of the reduced matrix elements of the individual operators in the uncoupled representation by
of these two irreducible operators in the coupled representation is given
in terms of the reduced matrix elements of the individual operators in the uncoupled representation by
|
|
|
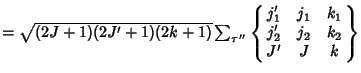
|
|
|
|
(1) |
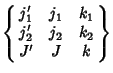 is a Wigner
is a Wigner
Shore and Menzel (1968) give the explicit formulas
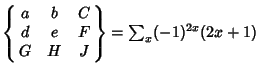
|
|
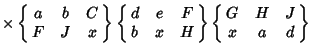
|
(2) |
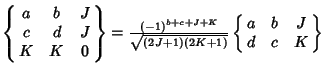
|
(3) |
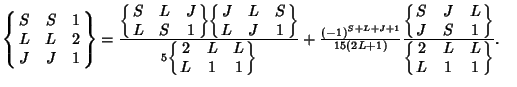
|
(4) |
See also Clebsch-Gordan Coefficient, Racah V-Coefficient, Racah W-Coefficient, Wigner 3j-Symbol, Wigner 6j-Symbol
References
Gordy, W. and Cook, R. L. Microwave Molecular Spectra, 3rd ed. New York: Wiley, pp. 807-809, 1984.
Messiah, A. ```
Shore, B. W. and Menzel, D. H. Principles of Atomic Spectra. New York: Wiley, pp. 279-284, 1968.
![]() ' Symbols.'' Appendix C.III in Quantum Mechanics, Vol. 2. Amsterdam, Netherlands: North-Holland, pp. 567-569
and 1066-1068, 1962.
' Symbols.'' Appendix C.III in Quantum Mechanics, Vol. 2. Amsterdam, Netherlands: North-Holland, pp. 567-569
and 1066-1068, 1962.