A set of four Paradoxes dealing with counterintuitive aspects of continuous space and time.
- 1. Dichotomy paradox: Before an object can travel a given distance
 , it must travel a distance
, it must travel a distance 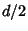 .
In order to travel
.
In order to travel 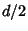 , it must travel
, it must travel 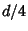 , etc. Since this sequence goes on forever, it therefore appears that
the distance
, etc. Since this sequence goes on forever, it therefore appears that
the distance  cannot be traveled. The resolution of the paradox awaited Calculus and the proof that
infinite Geometric Series such as
cannot be traveled. The resolution of the paradox awaited Calculus and the proof that
infinite Geometric Series such as
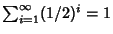 can converge, so that the infinite number of
``half-steps'' needed is balanced by the increasingly short amount of time needed to traverse the distances.
can converge, so that the infinite number of
``half-steps'' needed is balanced by the increasingly short amount of time needed to traverse the distances.
- 2. Achilles and the tortoise paradox: A fleet-of-foot Achilles is unable to catch a plodding tortoise which has been
given a head start, since during the time it takes Achilles to catch up to a given position, the tortoise has moved
forward some distance. But this is obviously fallacious since Achilles will clearly pass the tortoise!
The resolution is similar to that of the dichotomy paradox.
- 3. Arrow paradox: An arrow in flight has an instantaneous position at a given instant of time. At that
instant, however, it is indistinguishable from a motionless arrow in the same position, so how is the motion
of the arrow perceived?
- 4. Stade paradox: A paradox arising from the assumption that space and time can be divided only by a definite amount.
References
Pappas, T. ``Zeno's Paradox--Achilles & the Tortoise.'' The Joy of Mathematics.
San Carlos, CA: Wide World Publ./Tetra, pp. 116-117, 1989.
Russell, B. Our Knowledge and the External World as a Field for Scientific Method in Philosophy.
New York: Routledge, 1993.
Salmon, W. (Ed.). Zeno's Paradoxes. New York: Bobs-Merrill, 1970.
Stewart, I. ``Objections from Elea.'' In From Here to Infinity: A Guide to Today's Mathematics.
Oxford, England: Oxford University Press, p. 72, 1996.
vos Savant, M. The World's Most Famous Math Problem. New York: St. Martin's Press, pp. 50-55, 1993.
© 1996-9 Eric W. Weisstein
1999-05-26