Successive application of Archimedes' Recurrence Formula gives the Archimedes algorithm, which can be used to
provide successive approximations to 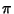 (Pi). The algorithm is also called the Borchardt-Pfaff
Algorithm. Archimedes obtained the first rigorous approximation of
(Pi). The algorithm is also called the Borchardt-Pfaff
Algorithm. Archimedes obtained the first rigorous approximation of 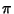 by Circumscribing and Inscribing
by Circumscribing and Inscribing 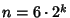 -gons on a Circle. From Archimedes'
Recurrence Formula, the Circumferences
-gons on a Circle. From Archimedes'
Recurrence Formula, the Circumferences 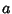 and
and 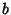 of the circumscribed and
inscribed Polygons are
of the circumscribed and
inscribed Polygons are
where
 |
(3) |
For a Hexagon, 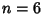 and
and
where
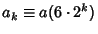 . The first iteration of Archimedes' Recurrence Formula then gives
. The first iteration of Archimedes' Recurrence Formula then gives
Additional iterations do not have simple closed forms, but the numerical approximations for 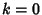 , 1, 2, 3, 4 (corresponding to
6-, 12-, 24-, 48-, and 96-gons) are
, 1, 2, 3, 4 (corresponding to
6-, 12-, 24-, 48-, and 96-gons) are
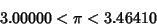 |
(8) |
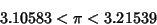 |
(9) |
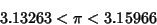 |
(10) |
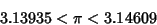 |
(11) |
 |
(12) |
By taking  (a 96-gon) and using strict inequalities to convert irrational bounds to rational bounds at each step,
Archimedes obtained the slightly looser result
(a 96-gon) and using strict inequalities to convert irrational bounds to rational bounds at each step,
Archimedes obtained the slightly looser result
 |
(13) |
References
Miel, G. ``Of Calculations Past and Present: The Archimedean Algorithm.'' Amer. Math. Monthly 90, 17-35, 1983.
Phillips, G. M. ``Archimedes in the Complex Plane.'' Amer. Math. Monthly 91, 108-114, 1984.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() (Pi). The algorithm is also called the Borchardt-Pfaff
Algorithm. Archimedes obtained the first rigorous approximation of
(Pi). The algorithm is also called the Borchardt-Pfaff
Algorithm. Archimedes obtained the first rigorous approximation of ![]() by Circumscribing and Inscribing
by Circumscribing and Inscribing ![]() -gons on a Circle. From Archimedes'
Recurrence Formula, the Circumferences
-gons on a Circle. From Archimedes'
Recurrence Formula, the Circumferences ![]() and
and ![]() of the circumscribed and
inscribed Polygons are
of the circumscribed and
inscribed Polygons are


![]() (a 96-gon) and using strict inequalities to convert irrational bounds to rational bounds at each step,
Archimedes obtained the slightly looser result
(a 96-gon) and using strict inequalities to convert irrational bounds to rational bounds at each step,
Archimedes obtained the slightly looser result