The best known example of an Anosov Diffeomorphism. It is given by the Transformation
![\begin{displaymath}
\left[{\matrix{x_{n+1} \cr y_{n+1}\cr}}\right] = \left[{\mat...
...\cr 1 & 2 \cr}}\right]\left[{\matrix{x_n \cr y_n \cr}}\right],
\end{displaymath}](a_1706.gif) |
(1) |
where  and
and  are computed mod 1. The Arnold cat mapping is non-Hamiltonian, nonanalytic, and mixing.
However, it is Area-Preserving since the Determinant is 1. The Lyapunov
Characteristic Exponents are given by
are computed mod 1. The Arnold cat mapping is non-Hamiltonian, nonanalytic, and mixing.
However, it is Area-Preserving since the Determinant is 1. The Lyapunov
Characteristic Exponents are given by
 |
(2) |
so
 |
(3) |
The Eigenvectors are found by plugging  into the Matrix Equation
into the Matrix Equation
![\begin{displaymath}
\left[{\matrix{1-\sigma_\pm & 1 \cr 1 & 2-\sigma_\pm \cr}}\r...
...trix{x\cr y \cr}}\right] = \left[{\matrix{0\cr 0 \cr}}\right].
\end{displaymath}](a_1712.gif) |
(4) |
For 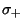 , the solution is
, the solution is
 |
(5) |
where 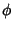 is the Golden Ratio, so the unstable (normalized) Eigenvector is
is the Golden Ratio, so the unstable (normalized) Eigenvector is
![\begin{displaymath}
\boldsymbol{\xi}_+ = {\textstyle{1\over 10}}\sqrt{50-10\sqrt{5}}\,\left[{\matrix{1 \cr {1\over 2}(1+\sqrt{5}\,)\cr}}\right].
\end{displaymath}](a_1715.gif) |
(6) |
Similarly, for  , the solution is
, the solution is
 |
(7) |
so the stable (normalized) Eigenvector is
![\begin{displaymath}
\boldsymbol{\xi}_- = {\textstyle{1\over 10}}\sqrt{50+10\sqrt{5}}\,\left[{\matrix{1 \cr {1\over 2}(1-\sqrt{5}\,)\cr}}\right].
\end{displaymath}](a_1718.gif) |
(8) |
See also Anosov Map
© 1996-9 Eric W. Weisstein
1999-05-25