The Apodization Function
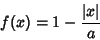 |
(1) |
which is a generalization of the one-argument Triangle Function. Its Full Width at Half Maximum is  .
It has Instrument Function
.
It has Instrument Function
Letting 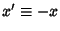 in the first part therefore gives
in the first part therefore gives
Rewriting (2) using (3) gives
Integrating the first part and using the integral
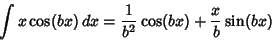 |
(5) |
for the second part gives
where
 is the Sinc Function. The peak (in units of
is the Sinc Function. The peak (in units of  ) is 1. The function
) is 1. The function 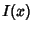 is always positive, so
there are no Negative sidelobes. The extrema are given by letting
is always positive, so
there are no Negative sidelobes. The extrema are given by letting
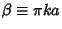 and solving
and solving
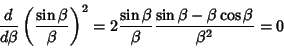 |
(7) |
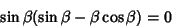 |
(8) |
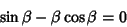 |
(9) |
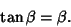 |
(10) |
Solving this numerically gives 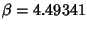 for the first maximum, and the peak Positive sidelobe is 0.047190. The
full width at half maximum is given by setting
for the first maximum, and the peak Positive sidelobe is 0.047190. The
full width at half maximum is given by setting
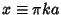 and solving
and solving
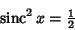 |
(11) |
for  , yielding
, yielding
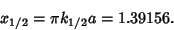 |
(12) |
Therefore, with 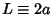 ,
,
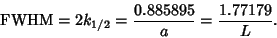 |
(13) |
See also Apodization Function, Parzen Apodization Function, Triangle Function
References
Bartlett, M. S. ``Periodogram Analysis and Continuous Spectra.'' Biometrika 37, 1-16, 1950.
© 1996-9 Eric W. Weisstein
1999-05-26

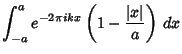


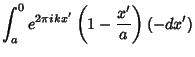
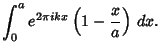
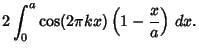
![$\displaystyle 2\left[{{\sin(2\pi kx)\over 2\pi k}-{1\over a}\left\{{{1\over 4\pi^2 k^2}\cos(2\pi kx)+{x\over 2\pi k}\sin(2\pi kx)}\right\}}\right]_0^a$](b_186.gif)
![$\displaystyle 2\left\{{\left[{{\sin(2\pi ka)\over 2\pi k}-0}\right]-{1\over a}\...
...{\cos(2\pi ka)-1\over 4\pi^2 k^2}+{a\sin(2\pi ka)\over 2\pi k}}\right]}\right\}$](b_187.gif)
![$\displaystyle {1\over 2\pi^2 ak^2} [\cos(2\pi ka)-1] = a{\sin^2(\pi ka)\over \pi^2 k^2a^2}$](b_188.gif)