|
|
|
Let ![]() and
and ![]() be Real Numbers (usually taken as
be Real Numbers (usually taken as ![]() and
and ![]() ). The Dirichlet function is
defined by
). The Dirichlet function is
defined by
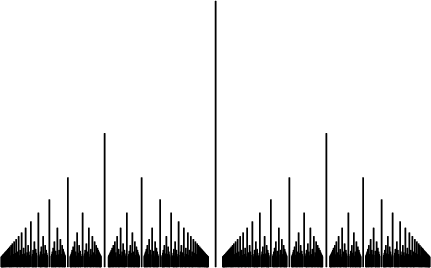
Because the Dirichlet function cannot be plotted without producing a solid blend of lines, a modified version can be defined as
See also Continuous Function, Irrational Number, Rational Number
References
Dixon, R. Mathographics. New York: Dover, pp. 177 and 184-186, 1991.
Tall, D. ``The Gradient of a Graph.'' Math. Teaching 111, 48-52, 1985.