|
|
|
A function built up of compositions of algebraic functions, the Exponential Function and the Trigonometric Functions and their inverses by Addition, Multiplication, Division, root extractions (the Elementary Operations) under repeated compositions (Shanks 1993, p. 145). Unfortunately, there are several different definitions of what constitutes an elementary function.
Following Liouville, Watson (1966, p. 111) defines
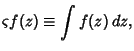 |
Not all functions are elementary. For example, the Normal Distribution Function
See also Algebraic Function, Elementary Operation, Elementary Symmetric Function, Transcendental Function
References
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, 1993.
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University
Press, p. 111, 1966.