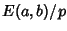 denotes the elliptic Group modulo
denotes the elliptic Group modulo 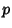 whose elements are
whose elements are 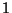 and
and 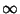 together with the pairs of
Integers
together with the pairs of
Integers 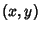 with
with 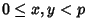 satisfying
satisfying
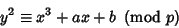 |
(1) |
with  and
and  Integers such that
Integers such that
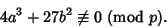 |
(2) |
Given 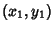 , define
, define
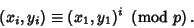 |
(3) |
The Order 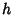 of
of 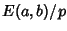 is given by
is given by
![\begin{displaymath}
h=1+\sum_{x=1}^p \left[{\left({x^3+ax+b\over p}\right)+1}\right],
\end{displaymath}](e_829.gif) |
(4) |
where 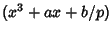 is the Legendre Symbol, although this Formula quickly becomes impractical. However, it
has been proven that
is the Legendre Symbol, although this Formula quickly becomes impractical. However, it
has been proven that
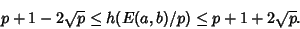 |
(5) |
Furthermore, for 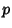 a Prime
a Prime 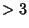 and Integer
and Integer  in the above interval, there exists
in the above interval, there exists  and
and  such that
such that
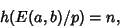 |
(6) |
and the orders of elliptic Groups mod 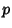 are nearly uniformly distributed in the interval.
are nearly uniformly distributed in the interval.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() denotes the elliptic Group modulo
denotes the elliptic Group modulo ![]() whose elements are
whose elements are ![]() and
and ![]() together with the pairs of
Integers
together with the pairs of
Integers ![]() with
with ![]() satisfying
satisfying
![\begin{displaymath}
h=1+\sum_{x=1}^p \left[{\left({x^3+ax+b\over p}\right)+1}\right],
\end{displaymath}](e_829.gif)