|
|
|
The term energy has an important physical meaning in physics and is an extremely useful concept. A much more abstract
mathematical generalization is defined as follows. Let ![]() be a Space with Measure
be a Space with Measure ![]() and let
and let
![]() be a real function on the Product Space
be a real function on the Product Space
![]() . When
. When
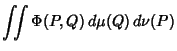 |
|||
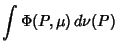 |
See also Dirichlet Energy, Mutual Energy
References
Iyanaga, S. and Kawada, Y. (Eds.). ``General Potential.'' §335.B in
Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1038, 1980.